Es ist tatsächlich wahr, auf fast triviale Weise. Das Ehrenfest-Theorem besagt, dass \ begin {Gleichung} \ frac {d} {dt} \ langle x \ rangle = \ langle p \ rangle, \ quad \ frac {d} {dt} \ langle p \ rangle = - \ langle V '(x) \ rangle \ end {Gleichung} span> Für alle Eigenfunktionen für den harmonischen Oszillator $ \ langle x \ rangle = 0 $ span> (und daher $ \ langle V '( x) \ rangle = 0 $ span>) und $ \ langle p \ rangle = 0 $ span>. Der Ehrenfest-Satz über die Eigenzustände reduziert sich also auf $ 0 = 0 $ span>.

Sie können sehen, dass die allgemeine Version des Ehrenfest-Theorems für alle Eigenzustände trivial funktioniert. Es besagt, dass für den willkürlich beobachtbaren $ A $ span> sein Erwartungswert die Gleichung erfüllt, \ begin {Gleichung} \ frac {d} {dt} \ langle A \ rangle = \ frac {1} {i \ hbar} \ langle [A, H] \ rangle + \ langle \ frac {\ partielles A} {\ partielles t} \ rangle \ end {Gleichung} span> Auf den Eigenzuständen jedoch \ begin {Gleichung} \ langle \ psi_n | [A, H] | \ psi_n \ rangle = \ langle \ psi_n | AH-HA | \ psi_n \ rangle = E_n \ langle \ psi_n | A-A | \ psi_n \ rangle = 0 \ end {Gleichung} span> Der Erwartungswert des Observablen, der nicht explizit von der Zeit abhängt, entwickelt sich also nicht auf den Eigenzuständen, was Sie erwarten würden.

Wohin führt das Ehrenfest-Theorem zur klassischen Dynamik? Sie müssen die lokalisierten Wellenpakete berücksichtigen. Das einfachste Beispiel wäre der kohärente Zustand des harmonischen Oszillators, der das Gaußsche Wellenpaket ist, das der klassischen Trajektorie folgt

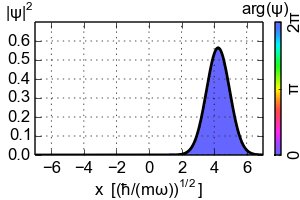
Für den harmonischen Oszillator ist der Satz von Ehrenfest immer "klassisch", wenn auch nur auf triviale Weise (wie im Fall der Eigenzustände).Im Allgemeinen reduziert sich das Ehrenfest-Theorem jedoch nur auf solche lokalisierten Wellenpakete auf die klassische Bewegungsgleichung, die sich in der Nähe der klassischen Trajektorie konzentrieren, wenn $ \ hbar $ span> auf Null geht.Der entscheidende Punkt ist zufällig der Austausch $ \ langle V '(x) \ rangle \ mapsto V' (\ langle x \ rangle) $ span>, der bei allgemeinen Zuständen möglich ist.nicht getan werden.Wenn Sie also eine klassische Dynamik aus der Quantentheorie wiederherstellen möchten, schauen Sie sich die lokalisierten Wellenpakete an.

1. Ihre Version von $ \ psi $ span> ist (wie Sie sicher wissen) aus der zeitunabhängigen Schrödinger-Gleichung $ \ hat {H} \ psi = E \ psi $ span>. Um zeitabhängige Lösungen zu finden, lösen wir $$ i \ frac {\ partiell} {\ partiell t} \ psi = \ hat {H} \ psi. $$ span> Sie haben versucht, nach stationären Zuständen zu suchen, und der springende Punkt dabei ist, dass sich $ | \ psi (x) | ^ 2 $ span> im Laufe der Zeit nicht ändert. Für diese Lösungen für stationäre Lösungen gilt jedoch $$ \ frac {\ mathrm {d}} {\ mathrm {d} t} \ left<x \ right> = \ left<p \ right> = 0; \ frac {\ mathrm {d}} {\ mathrm {d} t} \ left<p \ right> = - \ left< \ frac {\ mathrm {d}} {\ mathrm {d} x} V (x) \ right> = 0 , $$ span>, was dem Ehrenfest-Theorem entspricht (wenn auch nicht informativ).

2. Achten Sie auf die Zeitabhängigkeit Ihres gemeldeten $ \ psi $ span>: Sie haben es tatsächlich mit zu tun $ \ Psi (x, t) = \ psi (x) e ^ {- itE / \ hbar} $ span> für diese stationären Zustände. Dies bezieht sich natürlich nicht auf das Ehrenfest-Theorem, aber es ist erwähnenswert: Die komplexen und realen Teile schwingen, wie die rosa und blauen Linien in diesem Diagramm zeigen (von der Wikipedia-Seite auf QHO):

   Machen Sie nicht den Fehler zu behaupten, dass alle zeitlichen Ableitungen notwendigerweise automatisch gleich Null sind, da die Wellenfunktion zeitunabhängig ist. Im Gegensatz zu der Kurzschreibweise haben wir ein (trennbares) zeitabhängiges Bit.

3. Beobachten Sie unter Bezugnahme auf dasselbe Diagramm die Teile G und H: Diese stellen kohärente Zustände dar, die mit dem Satz von Ehrenfest verstanden werden können, weil $ |\ psi | ^ 2 $ span> sieht aus wie ein Gaußscher Wert, der einem klassischen $ \ sin $ span> oder $ \ cos folgt$ span> -Funktion.

ol>

Siehe

Kanasugi, H. und H. Okada."Systematische Behandlung des allgemeinen zeitabhängigen harmonischen Oszillators in der klassischen und Quantenmechanik." Fortschritt der Theoretischen Physik , vol.93, nein.5, 1995, S. 949–960., Doi: 10.1143 / ptp / 93.5.949.

Was Sie aufgeschrieben haben, ist nur ein vollständiger Satz von Lösungen der zeitunabhängigen Schrödinger-Gleichung. \ begin {align} [- \ frac {\ hbar²} {2m} \ Delta + V (x)] \ Psi (x) = E \ Psi (x) \ end {align} span> Natürlich sind diese Lösungen nicht zeitabhängig, da die zeitunabhängige Schrödinger-Gleichung (in dieser Darstellung) nur Aussagen über Funktionen macht, die nur von den Raumkoordinaten abhängen (in diesem Fall ist dies nur x).

Wie komme ich zu den zeitabhängigen Lösungen? Eine besondere Eigenschaft der Lösungen $ \ Psi_ {E} $ span> der zeitunabhängigen Schrödinger-Gleichung ist, dass $ \ Psi_ { E} (x) e ^ {- i \ frac {E} {\ hbar} t} $ span> ist eine Lösung für die zeitabhängige Schrödinger-Gleichung.

Wenn Sie dies auf Ihren Lösungsvorschlag des harmonischen Oszillators anwenden würden, würden Sie zu zeitabhängigen Lösungen gelangen. Dies sind diejenigen, über die das Ehrenfest-Theorem eine Aussage macht. Sie würden dann berechnen, dass sich die Erwartungswerte $ <X> $ span> und $ <P> $ span> nicht ändern. Sie können aber auch berechnen, dass beide Werte 0 sind. Dies stimmt perfekt mit den Theoremen von Ehrenfest überein, und das klassische Analogon wäre ein Teilchen, das an der tiefsten Stelle des harmonischen Potentials ruht.