Vermutlich wissen Sie bereits, dass sich der Schwerpunkt einer Partikelsammlung ohne äußere Kräfte mit konstanter Geschwindigkeit bewegt.Dies gilt unabhängig davon, ob sie in einem einzigen Körper zusammenkleben oder nur ein Bündel separater Körper mit oder ohne Wechselwirkungen zwischen ihnen sind.Wir bewegen uns nun zu einem Referenzrahmen, der sich mit dieser Geschwindigkeit bewegt.In diesem Rahmen ist das CofM stationär.

Nehmen wir nun an, dass die Partikel tatsächlich zu einem starren Körper zusammengeklebt sind.Wir sehen, dass sich der Körper so bewegt, dass: 1) das CofM fest bleibt, 2) alle Abstände zwischen den Partikeln fest sind.(Diese zweite Bedingung ist schließlich das, was mit einem $ starren $ Körper gemeint ist).

Eine Bewegung mit diesen beiden Eigenschaften (1) und (2) ist genau das, was mit dem Ausdruck "eine Drehung um das CofM" gemeint ist.

Hier ist eine weitere Möglichkeit, dies zu betrachten:

Sie können ein Objekt mit einer beliebigen Form als einen einzelnen Punkt betrachten, an dem die gesamte Masse des Objekts konzentriert ist.Dieser Punkt wird als Massenschwerpunkt bezeichnet.Nach dem zweiten Newtonschen Gesetz muss sich der Schwerpunkt entweder in einer geraden Linie bewegen oder stationär sein, da keine Kraft auf das Objekt wirkt.Wenn sich der Körper dreht, kann der Schwerpunkt diesem Gesetz nur folgen, wenn die Drehung um den Schwerpunkt erfolgt.

Stellen Sie sich zwei Steine vor, die mit einem masselosen Stab zusammengebunden sind, und lassen Sie einen Stein um den zweiten drehen, der fixiert wird.

In diesem Fall muss eine Kraft vorhanden sein, die den ersten Stein senkrecht zu seiner Geschwindigkeit beschleunigt und bewirkt, dass er sich um den zweiten dreht.Das gesamte Setup ist kostenlos, es gibt also keine Gegenkraft zum Ausgleich und dieses Setup verstößt gegen Newtons Gesetze.

Wenn wir diesen Stein-Stab-Stein-Körper in Bezug auf Newtons Gesetze drehen wollen, müssen wir einen beliebigen Punkt hinzufügen, um den er sich dreht.In diesem Fall drehen sich beide Steine um diesen Punkt, es wird eine Radialkraft auf beide ausgeübt und sie haben eine entgegengesetzte Richtung.Die Kräfte müssen sich vollständig aufheben und sie heben sich nur auf, wenn der beliebige Punkt genau im Schwerpunkt liegt.

Der Grund, warum sich ein Körper unter freier Rotation um seinen Massenschwerpunkt dreht, ist, dass das Trägheitsmoment des Tensors im Massenschwerpunkt minimal ist. Wenn Sie sich um einen Punkt drehen, der nicht der Schwerpunkt ist, müssen Sie den Satz der parallelen Achse anwenden.

$$ I '= I_ \ mathrm {CM} + m \ vec {r} _ \ mathrm {CM} ^ 2 $$

Das Minimum dieser Gleichung ist, wenn der Radius vom Schwerpunkt zur Rotationsachse Null ist. Daher ist der Schwerpunkt der Drehpunkt, der den geringsten Widerstand gegen Drehung bietet

Tatsächlich verschiebt sich das augenblickliche Rotationszentrum nicht augenblicklich in den Massenmittelpunkt des Objekts, sobald die äußeren Kräfte aufhören, auf das Objekt zu wirken. Stellen Sie sich vor, Sie haben eine Schüssel und lassen einen Ball hineinfallen, sodass der anfängliche Kontaktpunkt nahe am Rand liegt. Der Ball tendiert zum Boden der Schüssel, da dies der Ort mit dem niedrigsten Gravitationspotential ist. Bevor es dort ankommt, schwingt es jedoch ein wenig, bevor es zur Ruhe kommt. Der Boden der Schüssel ist ein stabiler Punkt.

Dies ist analog zu unserer Rotation. Der Punkt, um den sich das Objekt dreht, ist anfänglich vom Schwerpunkt versetzt. Mit fortschreitender Zeit tendiert es jedoch zum Schwerpunkt, wenn es versucht, den Weg des geringsten Widerstands zu finden. Eine Drehung um den Schwerpunkt liefert diesen geringsten Widerstand

Ich bin kein Physiker, aber ich werde es versuchen.

Ein vereinfachtes Beispiel für Ihre sich drehende Kugel, das Ihnen bei diesem Konzept helfen könnte, wäre eine Scheibe, die aus einer einzigen Materialdichte besteht. Ein Beispiel wäre ein Kinderoberteil oder ein Gyroskop, das Sie auf einer ebenen Fläche drehen können. Jeder Teil der Platte hat einen passenden Ausgleichsteil auf der gegenüberliegenden Seite der Platte. Jedes Ausgleichspaar von Teilen der Scheibe hat die gleiche Masse wie die anderen, hat beim Drehen entgegengesetzte Bewegungen zueinander und erzeugt entgegengesetzte Ausgleichszentripetalkräfte, die die Drehung der Scheibe um den Schwerpunkt (der auch das geometrische Zentrum der Scheibe ist) im Gleichgewicht halten. .

Wenn Sie der Disc irgendwo anders als in der Mitte mehr Masse hinzufügen, verschiebt sich der Massenmittelpunkt der Disc vom geometrischen Mittelpunkt der Disc weg und in Richtung der Masse, die Sie gerade hinzugefügt haben. Das Objekt dreht sich nun um diesen neuen Schwerpunkt. Dies liegt daran, dass die gesamte Masse auf der Seite, die von der neu hinzugefügten Masse entfernt ist, eine ausgleichende Gegenkraft zur jetzt schwereren Seite der Scheibe erzeugen muss. Die Masse der Scheibe zwischen dem geometrischen Mittelpunkt der Scheibe und dem neuen (verschobenen) Schwerpunkt verschiebt sich, um die der hinzugefügten Masse entgegengesetzte Ausgleichskraft zu werden

Das folgende Bild kann Ihnen dabei helfen, dies zu veranschaulichen:

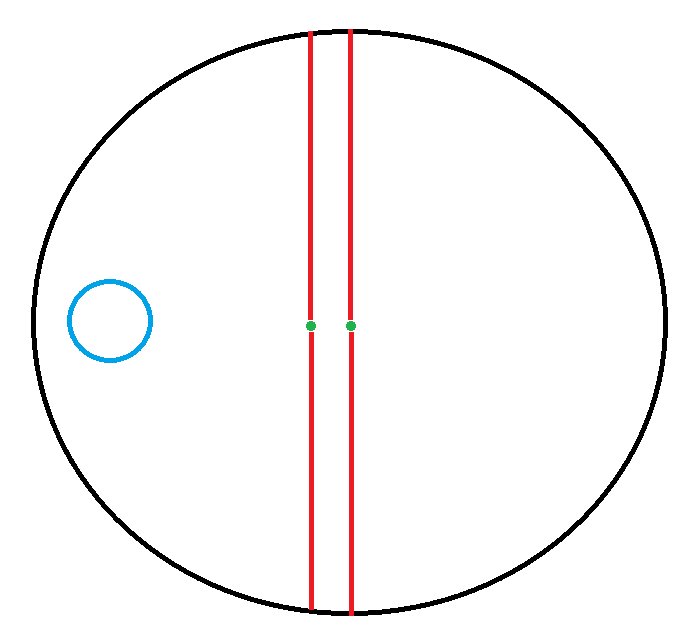
Der grüne Punkt rechts ist der ursprüngliche Schwerpunkt und der Mittelpunkt der Disc. Der blaue Kreis ist eine zusätzliche Masse. Der grüne Punkt links ist der neue Schwerpunkt. Der Bereich zwischen den beiden roten Linien ist die Masse auf der Scheibe, die die hinzugefügte Masse beim Drehen ausgleicht. Durch Hinzufügen von mehr (blauer) Masse wird der Schwerpunkt weiter vom ursprünglichen Mittelpunkt entfernt und die linke rote Linie (und der Schwerpunkt) weiter in Richtung der hinzugefügten Masse (links) verschoben. Wenn die ursprüngliche Scheibe im Verhältnis zur hinzugefügten Masse sehr massiv war, verschiebt sich der Schwerpunkt nicht so weit (dh weniger Fläche zwischen den roten Linien, die zum Ausgleich der neuen Masse erforderlich sind, und weniger Verschiebung des Schwerpunkts zum Ausgleich der hinzugefügten Masse ).

Zusammenfassend lässt sich sagen, dass jedes Mal, wenn Sie die Masse eines rotierenden Objekts addieren (oder von dieser subtrahieren), das Objekt den Ort seines Rotationszentrums ändert, sodass die durch die Rotation verursachten Kräfte im Gleichgewicht bleiben.Der Drehpunkt ist der Mittelpunkt der gesamten Masse dieses Objekts.

Ich dachte, dass die Bewegung um die COM die stabilste ist und die Rotation um andere Punkte degeneriert. Ich denke nicht, dass es richtig ist. Ist es?

Lassen Sie uns für eine Sekunde damit fortfahren. Ich bin mir nicht sicher, ob der Begriff "entartet" es hier völlig entartet, aber ich denke, Sie sind auf dem richtigen Weg. Stellen Sie sich ein perfekt ausbalanciertes Rad in einem Auto vor. Seine Drehung ist nicht frei, sondern fest in seiner Mitte, die auch sein Schwerpunkt ist (weil es ausgeglichen ist). Wenn es sich dreht, gibt es keine Kraft auf die Achse.

Überlegen Sie nun, was passiert, wenn wir ein Gewicht an der Felge des Rads anbringen und es aus dem Gleichgewicht bringen. Wenn sich das Rad dreht, übt es nun Kräfte auf die Achse aus. Wenn Sie jemals in einer solchen Situation in einem Fahrzeug gefahren sind, werden Sie dies bei den meisten Geschwindigkeiten als Vibration empfinden, da das Rad ständig "springt". Warum passiert das? Dies liegt daran, dass die Achse das Rad zwingt, sich um einen Punkt zu drehen, der nicht sein Schwerpunkt ist. Mit anderen Worten, nur die Drehung um den Schwerpunkt ist neutral; Damit sich ein Objekt um einen anderen Punkt drehen kann, ist eine andere Kraft erforderlich, um es an Ort und Stelle zu halten. Per Definition unterliegt ein "freies" Objekt keiner solchen Kraft.

Eine Möglichkeit, dies zu sehen, besteht darin, einen Frisbee zu nehmen und ihn um einen Finger im Rand zu drehen. Es dreht sich um Ihren Finger (der sich nicht im Zentrum seiner Masse befindet). Ihre Muskeln müssen der Bewegung ständig widerstehen, um sie an Ort und Stelle zu halten. Wenn Sie Ihren Finger plötzlich entfernen, fliegt er in einer geraden Linie ab und dreht sich weiter um seinen Schwerpunkt.

Da das Trägheitsmoment beim Drehen um den Schwerpunkt minimal ist, "durchläuft" jede auf den Körper ausgeübte Kraft den "Pfad" mit minimalem Widerstand.

Grundsätzlich ist es der Punkt, für den die Summe aller Impulse minimal ist.

Auch Wasser und elektrischer Strom fließen über Wege mit minimalem Widerstand. Ich wollte absichtlich eine kurze Antwort geben, weil ich denke, dass die alternative Antwort nur ein "Zeigen Sie die Berechnungen" ist, was nicht sehr intuitiv ist.

Tatsächlich dreht sich ein Festkörper nicht um einen Punkt (COM), sondern um eine Achse, auf der sich der COM befindet.

Zum Beispiel in einer festen, gleichmäßigen Kugel (jedes Objekt mit einer ungleichmäßigen Massenverteilung kann kontinuierlich in eine Kugel mit derselben gleichmäßig verteilten Masse transformiert werden) liegen die einzigen Punkte, die sich um die COM drehen, in der Äquatorebene senkrecht zur Drehachse. Alle anderen Punkte drehen sich um einen anderen Punkt auf der Drehachse.

Wenn Sie die Kugel von einer Winkelgeschwindigkeit von Null zu einer Winkelgeschwindigkeit x drehen lassen, ohne der Kugel einen linearen Impuls zu verleihen, kann der lineare Impuls nur erhalten werden, wenn alle Momente der dm (unendlich kleine Massen, wenn wir die Kugel betrachten) als kontinuierliche Masse) abbrechen, was der Fall ist, wenn der COM auf der Drehachse liegt. Wenn Sie verschiedene Rotationsachsen berücksichtigen, haben diese natürlich den COM-Punkt gemeinsam.

Für zwei getrennte Körper, die durch eine Anziehungskraft als Schwerkraft begrenzt sind, kann man sagen, dass sich die Körper um die COM der beiden Körper drehen. Wie zwei Massen, die durch ein Seil verbunden sind, aber das Seil entfernt haben. In diesem Fall dreht sich die Drehung ebenfalls um die Rotationsachse (senkrecht zur Rotationsebene), aber auch um den COM-Punkt.

Ich verstehe dies eher als mathematisches oder psychologisches als als als physisches Phänomen.

Ein Objekt kann sich um eine beliebige Achse drehen. In dem Fall, in dem die Achse nicht durch den Schwerpunkt verläuft, zerlegen wir diese Bewegung normalerweise in eine Bewegung des Schwerpunkts des Objekts, kombiniert mit einer Bewegung um den Schwerpunkt. Sie können dies immer tun. Fragen Sie einfach: "Wie hat sich der Schwerpunkt bewegt?" und subtrahieren Sie diese Bewegung von der Bewegung jedes Stücks. Per Definition ist die verbleibende Bewegung eine Drehung um den festen Schwerpunkt.

Wir müssen die Bewegung nicht auf diese Weise unterbrechen. Es kommt also vor, dass wir (in der Newtonschen Mechanik) wissen, wie man mit Impuls und Drehimpuls getrennt umgeht. Unterschiedliche Zerlegungen wären möglich. Aber sie wären mit ziemlicher Sicherheit komplexer und weniger intuitiv. Nehmen wir zum Beispiel an, dass der Drehimpuls immer zu einer zusätzlichen "linearen Kraft" führte, die gerichtet war und von der Beziehung zwischen der Massenverteilung und der Achse abhing. Es wäre viel schwieriger zu verstehen, woraus es tatsächlich bestand. Wir sind es gewohnt, Dinge um ihren Schwerpunkt zu drehen.

Wenn Sie Newtonsche Drehmomentprobleme lösen, müssen Sie normalerweise mit Bedacht einen Punkt auswählen, um die Drehmomente zu lösen. Die Lösung wäre dieselbe, aber die Technik ist viel einfacher, wenn Sie den richtigen Punkt auswählen, für den sich so viele Kräfte wie möglich aufheben. 'Schwerpunkt' ist nur die Standardheuristik für den allgemeinen Fall dieses Problems.

Wie Sie aus dem Fahrradfahren wissen, ist es möglich, mit einer sehr langsamen Geschwindigkeit zu balancieren, ohne zu fallen, wenn Sie das Gewicht auf beiden Seiten gleichmäßig ausbalancieren können. Wie bei einer Wippe. Es stellt sich heraus, dass Sie immer einen Weg finden können, einen starren Körper auszugleichen, unabhängig davon, wie er die darunter liegende Oberfläche berührt, indem Sie die Masse genau richtig platzieren, damit sie gleichmäßig verteilt ist.

Hier sehen Sie ein Video, wie dies gemacht werden kann: https://www.youtube.com/watch?v=OGRUf1PLJdY

Wenn Sie jetzt erkennen, dass dies wahr ist, unabhängig davon, wie der starre Körper überhaupt ausgerichtet ist, müssen Sie nur überlegen, ob all diese Trennlinien "die Masse in gleiche Teile teilen" etwas gemeinsam haben oder nicht. Es stellt sich heraus, dass sie alle einen einzigen gemeinsamen Punkt durchlaufen (dies kann mathematisch bewiesen werden), von dem Sie wahrscheinlich bereits vermutet haben, dass er den Schwerpunkt benannt hat.

Es kann auch mathematisch bewiesen werden, dass sich ein starrer Körper genauso verhält wie ein einzelner Punkt mit der vollen Masse des starren Körpers. Dies erleichtert Newtonsche Berechnungen (wie die Bewegung der Erde um die Sonne).

Damit das Paar um die Schwerpunktachse gleichmäßig verteilt wird, damit sich der Körper drehen kann.Da die Rotation selbst als Rotationsachse definiert ist und der Schwerpunkt in derselben Linie liegen sollte, dreht sie sich um die Rotationsachse.
Der andere Grund ist, dass die Rotation aufrechterhalten werden kann.