Nein, es gibt keine ähnliche Aussage in der Physik und kann es auch nicht geben.Das liegt daran, dass wir alles über die mathematischen Systeme wissen können, die wir konstruieren.Immerhin haben wir sie selbst eingerichtet (aber dann sagt uns Gödels Unvollständigkeitssatz, dass es Merkmale bestimmter Systeme geben kann, die nicht erkennbar sind; es tut mir leid, dass wir geschlachtet haben, was der Satz wirklich sagt, übrigens).

Die Physik hingegen versucht letztendlich, die Realität zu modellieren.Das Problem dort ist, dass wir grundsätzlich keine Möglichkeit haben, die Realität an sich zu erkennen.Wir können nicht einmal sicher sein, dass es so etwas wie Realität gibt, obwohl wir dies als grundlegendes Axiom der Physik betrachten.Wir können also nur Modelle für die Realität vorschlagen, die wir erleben.Wir können nicht wissen, in welchem Verhältnis solche Modelle zur Realität stehen.

Ich werde diese Frage zuerst ein wenig ändern. Betrachten Sie Quantenzustände als Quanteninformationen oder Quantenbits, die von Turing-Maschinen (TM) verarbeitet werden, die von Hamiltonianern gesteuert werden. Wir können uns den Löschprozess des Entfernens von Symbolen in einer Turing-Maschinenbewegung als mit Hilfsregistern wiederhergestellt vorstellen, so dass irreversible Prozesse ein Problem sind, das vermieden werden kann. Ich würde sagen, es ist besser darüber nachzudenken, ob die von Alan Turing nachgewiesene algorithmische Unvollständigkeit vorliegt, dass es keine universelle Turing-Maschine (UTM) gibt, die den Stoppstatus bestimmen kann, oder wie sich herausstellt, eine Reihe anderer Merkmale mögliche Turingmaschinen, gilt für die quantenmechanische Evolution. Wir haben also einige Hamilton-Werte. Wenn das System lie-algebraisch ist, ist dies durch das Produkt von Wurzeln gegeben, die als Anhebungs- und Absenkoperatoren fungieren, und das System entwickelt sich in einer Lehrbuchform. Kann es eine algorithmische Unvollständigkeit geben?

Ich werde zunächst sagen, dass die meisten Physiker entweder mit den Schultern zucken oder tatsächlich ziemlich „gereizt“ über den Vorschlag werden. Die meisten Physiker denken eher nicht. Wenn die Mehrheit der Physiker dies denkt und Sie nichts anderes zu tun haben, dann denken Sie auf jeden Fall zumindest über die Möglichkeit nach! Ich werde auch als zweite Meinung in diesem Absatz sagen, dass ich ehrlich gesagt keine Ahnung davon habe, aber warum nicht zumindest über die Möglichkeit nachdenken? Das Schlimmste, was passieren kann, ist, dass ich falsch liege.

Wo könnte diese Unvollständigkeit in der Physik auftreten? Ich würde sagen, eine Möglichkeit ist die Quantenmessung. Die Quantenmechanik ist perfekt deterministisch und berechnet die Entwicklung der Amplituden, deren Modulquadrat die Wahrscheinlichkeit von Ergebnissen bei einer Messung angibt. Wir haben jedoch keine Theorie darüber, wie ein Ergebnis tatsächlich erzielt wird. Hierfür gibt es keine Dynamik, und Versuche, dies zu tun, verstoßen gegen den Satz von Bell und andere Einschränkungen der Quantenmechanik. Doch die Natur bringt ein Ergebnis hervor! Quanteninterpretationen haben Löcher und reduzieren die Quantenmechanik effektiv auf metaphysische Kategorien, die zu kurz kommen. Wir können uns den Messprozess als eine Menge von Quantenzuständen vorstellen, die von einer anderen Menge von Quantenzuständen gemessen werden, normalerweise weitaus mehr Quantenzuständen, und am Ende ist dies eine Art selbstreferenzielle Schleife. Dies ähnelt einer UTM, die andere TMs emuliert, oder einem Prädikat, das auf Godel-Zahlen für Prädikate in Godels erstem Theorem einwirkt.

Um einen möglichen physikalischen Fall eines Systems zu geben, betrachten wir die Reissnor-Nordstrom-Metrik der Schwarzen Löcher (BH). Das folgende Penrose-Diagramm zeigt Null-Geodäten, die in das BH eintreten und sich in der Nähe von $ r _ + $ häufen. Angenommen, im Außenbereich befindet sich eine Drehmaschine, die ein Problem ohne Anhalten berechnet. Der unfehlbare Beobachter in einem ewigen Schwarzen Loch erfasst im Prinzip die Berechnung in einem endlichen Zeitraum. Der unfehlbare Beobachter oder Computer kann eine universelle Turingmaschine sein, die den Haltestatus einer möglichen Turingmaschine bestimmt. Dies ist eine Malament-Hogarth (MH) -Raumzeit, die als HyperTuring-Maschine in der Lage ist, nicht berechenbare Probleme zu lösen. Ein BH absorbiert im Prinzip Qubits und ermöglicht es Innenbeobachtern, abzuleiten, ob ein Problem zum Stillstand kommt oder nicht. 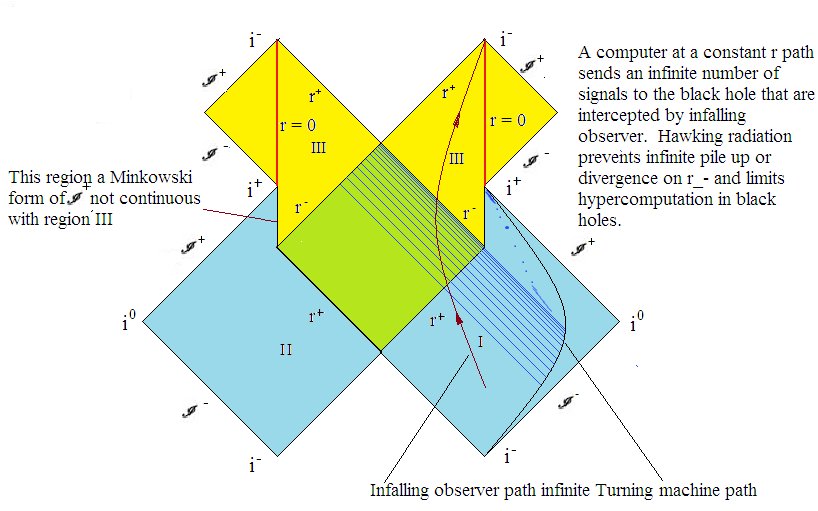Dieses Argument gilt für ein ewiges BH, während BHs in Wirklichkeit Hawking-Strahlung emittieren und nicht ewig sind. Auch solche BHs haben komplexe Quantenhaare. Das Diagramm wurde verfälscht, um dies zu veranschaulichen, wenn das BH eine endliche Dauer hat. Folglich kann ein BH mit Haaren nicht feststellen, ob alle möglichen Turing-Maschinen anhalten, aber er kann feststellen, ob eine signifikante Anzahl anhält. Dadurch wird die Chaitin-Stoppwahrscheinlichkeit in Bezug auf die Chaitin-Konstante angepasst. Ob eine Turingmaschine anhalten kann oder nicht, ist mit einer Wahrscheinlichkeit gegeben, die nicht universell berechenbar ist. Folglich wurden die Würfel auf eine nicht erkennbare Weise günstig geladen, um den Stoppstatus zu bestimmen. Eine physische Hyper-Turing-Maschine ist eine abgeschnittene Version des Ideals.

Möglicherweise hat der Satz von Godel eine Beziehung zum Bewusstsein. Douglas Hofstadter schrieb ein unterhaltsames Buch $ \ it Godel ~ Escher ~ Bach $, das die Idee des Bewusstseins als Selbstreferenz untersuchte. Goedels Theorem und Loebs Theorem erlauben es, Unbeweisbarkeit in modale Logik umzuwandeln, siehe Boolos Burgess und Jefferies „Berechenbarkeit und Logik“. Für $ \ square $ bedeutet dies notwendigerweise und ein Satz $ p $, dann ist $ \ square p ~ \ rightarrow ~ p $ wahr, aber der Satz von Godel zeigt an, dass $ \ existiert p: p ~ \ rightarrow ~ \ neg \ square p $. Dies ist ein Gegenbeispiel zu dem Argument, das Anslem für die Existenz Gottes vorbrachte. Dies bedeutet, dass ein Satz, der ein fester Punkt eines Prädikats ist, das aus nachweisbaren und wahren Funktionen aufgebaut ist, einer funktionalen Kombination falscher Aussagen entspricht. Dies bedeutet, dass in einem modalen Sinne $ \ neg \ square \ neg ~ = ~ \ Diamond $, was möglicherweise bedeutet, eine Art „Freiheit“ anzeigt, die in der Mathematik existiert. Im Sinne einer Berechnung kann ein System, wie beispielsweise eine abgeschnittene Hyper-Turing-Maschine, den Wahrheitswert von Sätzen anhand der Chaitin-Zahl $ \ Omega $ schätzen.

Es könnte sein, dass das Bewusstsein auch eine verkürzte Hyper-Turing-Maschine ist, die sich dem Ideal eines vollständig selbstreferenziellen Systems annähert, das „aus einem Algorithmus herausspringen“ oder einen Sprung in die Vorstellungskraft machen kann. Ein abgeschnittenes System kann diese Aktionen möglicherweise ausführen, jedoch nicht in einer vollständigen „gottähnlichen“ Form. Eine ideale Hyper-Turing-Maschine kann „trans-nachweisbare“ Operationen ausführen, einschließlich der Wahl zwischen nicht beweisbaren „Axiomen“, um ein Modell zu erstellen, das für die Funktion dieses Systems erforderlich ist. Für ein physikalisches System ist das System nicht perfekt, und dies kann bestenfalls unter den Grenzen unbeweisbarer Chaitin-Wahrscheinlichkeiten funktionieren. Es gibt dann eine Beziehung $ \ Diamond ~ \ leftrightarrow ~ \ Omega $, die innerhalb dieser Grenzen operiert. Die Tatsache, dass dies $ \ Diamond $ oder eine Möglichkeit beinhaltet, bedeutet, dass aus physikalischer Sicht eine relative Entropie von Zuständen besteht, die mit dieser Unsicherheit verbunden sind.

Dies berührt die Physik der Quantengravitation, und ich habe in vielerlei Hinsicht angenommen, dass die Fragen zur Dekohärenz der Wellenfunktion in Hawking-Strahlung Verbindungen zum Messproblem haben. Wir könnten dann darüber nachdenken, wo dies mit Mathe ins Spiel kommt. Das möglicherweise Freudenthal-System von Tripeln von $ E_8 $ oder $ {\ cal O} ^ 3 $ könnte eine Struktur sein, die der Stringtheorie zugrunde liegt. Diese enthält die $ 26 $ dimensionale Bosonische Saite und auch das Blutegelgitter. Das Blutegelgitter oder die sporadische Mathieu-Gruppe $ {\ cal M} _ {24} $ ist der Automorphismus der Fischer-Greiss-Monstergruppe. Es wurde festgestellt, dass dies wiederum Auswirkungen auf die Zahlentheorie hat, die als Mondschein oder Regenschirm-Mondschein bezeichnet wird. Mein schwarzer Hund, den ich Umbral nannte. Jetzt können wir dann sehen, wie auf subtile Weise in der Mathematik der Satz von Godel den Kopf aufrichten könnte.

Das ist also eher spekulativ, und ich weiß, dass es diejenigen geben wird, die damit nicht zufrieden sind. Menschen, die sich an die Regeln halten und immer das tun, was ihnen gesagt wurde, tauchen jedoch selten in der Geschichte auf.

Ich war lange Zeit fasziniert von einer Reihe von Theoremen, die die Grenze des erkennbaren Universums zu definieren scheinen. Und damit meine ich nicht nur die Grenze dessen, was wir heute wissen, um erweitert zu werden, wenn wir morgen mehr lernen. Ich meine die absoluten Grenzen von Wissenschaft und Vernunft, über die wir uns niemals hinaus wagen können, egal wie klug wir sind. Diese Grenzmeta-Theoreme umfassen Folgendes:

• Heisenbergs Unsicherheit (Physik) - Es gibt eine Grenze, wie genau können wir die Eigenschaften physikalischer Objekte messen.

Beachten Sie das letzte Wort in jedem Satznamen. Jeder von ihnen drückt ein Negativ aus. Jeder von ihnen erzählt uns etwas darüber, was wir nicht können, wohin wir nicht gehen können, was wir unter keinen Umständen wissen können. Die Intuition legt nahe, dass diese fünf Prinzipien trotz ihrer unterschiedlichen Anwendungsbereiche irgendwie miteinander verbunden sind. Tatsächlich scheinen sie genau gleich zu sein oder stammen zumindest aus demselben zugrunde liegenden Phänomen. Nämlich das: Grundlegende Zufälligkeit existiert. Es ist nicht nur eine kleine Warze in unserer logischen Welt, sondern ein unergründlicher Ozean, der sie umgibt. Wir können nie wissen, was in diesem Ozean der Zufälligkeit vor sich geht. Wir können nur einen Blick auf die Form der Küste unserer kleinen Insel der Vernunft werfen, da die oben aufgeführten Theoreme und Prinzipien zu leuchten beginnen.

Speziell für die Physik besagt das Heisenbergsche Unsicherheitsprinzip grundsätzlich, dass bestimmte Paare von Eigenschaften physikalischer Objekte - einfache Dinge wie wo sie sind und wie schnell sie sind - nicht gleichzeitig mit perfekter Präzision gemessen werden können. Je genauer Sie beispielsweise die Position eines Elektrons messen, desto weniger sicher können Sie im selben Moment über seine Geschwindigkeit sein. Wenn Sie die Position sehr, sehr, sehr sorgfältig messen, ist jede Zahl, die Sie für die Geschwindigkeit beobachten, im Wesentlichen bedeutungslos. es ist zufällig über eine bestimmte Anzahl von Dezimalstellen hinaus. Diese Grenze, wie genau man mit diesen kombinierten Messungen sein kann, ist für größere Objekte wie Bowlingkugeln oder BBs vernachlässigbar, aber für kleine Dinge wie Elektronen und Photonen macht es einen Unterschied. Die kombinierte Grenze unserer Messgenauigkeit wird durch die reduzierte Plankenkonstante bestimmt, die etwa 35 Dezimalstellen Genauigkeit beträgt. Darüber hinaus sind physikalische Eigenschaften allgemein nicht messbar.

HUP kann verstanden werden, indem man darüber nachdenkt, wie sich die Messungen auf das zu messende Objekt auswirken. Um die Position eines Elektrons zu messen, muss ein Licht darauf gerichtet werden, und für eine genauere Messung sind Photonen mit kürzerer Bandbreite und höherer Energie erforderlich. Wenn das Elektron von dem hochenergetischen Photon getroffen wird, wird seine Geschwindigkeit beeinflusst, wodurch Zufälligkeit eingeführt wird

Und so wurde es zunächst vorgestellt und besprochen, um die experimentelle Genauigkeit einzuschränken. Das Lehrbuch zur Quantenphysik, das ich im College verwendet habe, die 1974 erschienene Ausgabe der Quantenphysik von Eisberg und Resnick, erklärte das Unsicherheitsprinzip mit den Worten: "Unsere Messgenauigkeit ist von Natur aus durch den Messprozess selbst begrenzt [...]." Albert Einstein und viele andere prominente Zeitgenossen von Heisenberg glaubten, dass es immer noch eine Reihe von "verborgenen Variablen" geben muss, die das Universum kontrollieren und präzise, ​​deterministische Antworten auf jede Frage liefern, selbst wenn unsere Fähigkeit zur experimentellen Verifizierung für immer eingeschränkt war diese Antworten aufgrund des Unsicherheitsprinzips.

Einstein hat zusammen mit seinen Kollegen Boris Podolsky und Nathan Rosen sogar ein berühmtes Papier geschrieben, in dem sie fast spöttisch bewiesen haben, dass die Quantenmechanik falsch sein muss, sonst wäre die Welt, wie wir sie kennen, ein wirklich seltsamer Ort. Dazu nahmen sie nur zwei scheinbar offensichtliche Dinge über die Welt an. Erstens, dass Objekte intrinsische Eigenschaften wie Position und Geschwindigkeit haben, selbst wenn niemand sie misst. Dies nannten sie "Realität". Und zweitens können Messungen der Realität an einem Ort und zu einer Zeit andere, weit entfernte Realitäten nicht sofort beeinflussen, eine Eigenschaft, die sie "Lokalität" nannten. Einstein, Podolsky und Rosen sagten im Grunde, wer würde in einer Welt leben wollen, in der Realität und Lokalität nicht existierten. Mit anderen Worten, sie glaubten, unser freundliches, geordnetes Universum könne unmöglich von Natur aus zufällig sein.

But sie waren falsch.

1964 bewies Professor John Stewart Bell ein Ergebnis, das einige als "tiefgreifendste Entdeckung der Wissenschaft" bezeichneten. Der bescheidene Titel seines brillanten Papiers On the Einstein Podolsky Rosen Paradox bezog sich auf das von Einstein und seinen Freunden skizzierte "Paradox". Bell hat bewiesen, dass das Universum tatsächlich grundsätzlich von Natur aus zufällig ist. Genauer gesagt zeigte er, dass keine deterministische Theorie, die auf versteckten Variablen basiert, möglicherweise alle beobachteten Ergebnisse der Quantenmechanik erklären kann. Und wenn das bedeutet, dass es keine Realität oder Lokalität gibt, dann soll es so sein. Entweder das Prinzip der Realität oder das Prinzip der Lokalität (oder beides) gilt in unserem Universum nicht! Ein seltsamer Ort.

Heisenbergs Unsicherheitsprinzip ist nicht nur eine Grenze dafür, wie genau wir Dinge messen können. Es ist eine Grenze für das, was wir über das Universum wissen dürfen, in dem wir leben. Es gibt physikalische Größen, die allgemein unvorhersehbar sind. Das Fundament unserer vertrauten physischen Welt liegt der göttliche Zufall.

Lesen Sie mehr über The Divine Random.

Mathematik ist eine Sprache, die an die Grenzen von Objektivität und Präzision stößt, wo alle Konzepte klar definiert und miteinander verknüpft sind und ihre Artikulationen durch explizite Regeln geregelt werden.In diesem Zusammenhang stellt Gödels Theorem eine grundlegende Unvollständigkeit der Sprache selbst fest.

Solange wir Physik durch das definieren, was wir über die Welt wissen, unterliegt sie derselben Einschränkung: Sprache wird niemals vollständig genug sein, um die Welt zu beschreiben, weil Sprache in ihrem Wesen an sich begrenzt ist.

Jetzt ist Physik mehr als die Ausarbeitung einer Beschreibung der Realität: Es ist eine tatsächliche Interaktion mit der Realität auf immer subtileren und tieferen Ebenen.Es gibt keinen Hinweis auf eine harte Grenze für dieses Unterfangen.

Ja, in der Physik gibt es bestimmte "Unvollständigkeitssätze". Das, was ich kenne, ist die "Unentscheidbarkeit der spektralen Lücke" in der Quanten-Vielteilchenphysik. Ein kürzlich veröffentlichter Preprint sowie ein referiertes Papier in Nature beschreiben die Situation vollständiger. Nachstehend ist die Zusammenfassung des Papiers in Nature wiedergegeben, die eine bessere Zusammenfassung des Beweises liefert, als ich annehmen könnte.

Die spektrale Lücke - die Energiedifferenz zwischen dem Grundzustand und Der erste angeregte Zustand eines Systems ist von zentraler Bedeutung für das Quanten-Vielteilchen Physik. Viele herausfordernde offene Probleme, wie das Haldane Vermutung, die Frage nach der Existenz von lückenhaftem topologischem Spin Flüssige Phasen und die Yang-Mills-Lückenvermutung betreffen das Spektralspektrum Lücken. Diese und andere Probleme sind besondere Fälle des Allgemeinen Spektrallückenproblem: Angesichts des Hamilton-Operators eines Quanten-Vielteilchens System, ist es lückenhaft oder lückenlos? Hier beweisen wir, dass dies ein ist unentscheidbares Problem. Insbesondere konstruieren wir Quantenfamilien Spinsysteme auf einem zweidimensionalen Gitter mit translatorisch invariante Wechselwirkungen mit dem nächsten Nachbarn, für die die spektrale Lücke Problem ist unentscheidbar. Dieses Ergebnis erstreckt sich auf die Unentscheidbarkeit anderer Niedrigenergieeigenschaften wie das Vorhandensein von algebraisch zerfallenden Eigenschaften Grundzustandskorrelationen. Der Beweis kombiniert die Hamiltonsche Komplexität Techniken mit aperiodischen Fliesen, um einen Hamiltonianer zu konstruieren, dessen Der Grundzustand codiert die Entwicklung einer Quantenphasenschätzung Algorithmus gefolgt von einer universellen Turingmaschine. Die spektrale Lücke hängt vom Ergebnis des entsprechenden „Stoppproblems“ ab. Unsere Ergebnis impliziert, dass es keinen Algorithmus gibt, um zu bestimmen, ob ein Ein beliebiges Modell ist lückenhaft oder lückenlos und es gibt Modelle für wobei das Vorhandensein oder Fehlen einer Spektrallücke unabhängig von der ist Axiome der Mathematik.

Es gibt eine Frage, wie viel wir in der Physik wissen können, die derzeit die Leute stört, die die Quantengravitation studieren. Ich habe davon aus einem Vortrag von Nima Arkani-Hamed gehört (den Sie hier finden können), und die Idee ist ungefähr so:

In der relativistischen Quantenmechanik entsprechen Sondierungsphänomene mit einer hohen charakteristischen Energieskala der Sondierung von Skalen kurzer Länge. Experimente wie der LHC versuchen daher, so viel Energie wie möglich in einen möglichst kleinen Raumbereich zu packen, um immer massereichere (d. H. Energetische) Partikel zu finden.

Die mit der Schwerkraft verbundenen Energieskalen sind so hoch, dass niemand jemals hofft, sie mit einem Teilchenbeschleuniger zu erforschen. Es gibt jedoch ein noch grundlegenderes konzeptionelles Problem bei der Untersuchung der Quantengravitation, was darauf hindeutet, dass es möglicherweise nicht möglich ist, bestimmte Quantengravitationseffekte auch im Prinzip zu untersuchen: Um die notwendige Energiedichte zum Sehen von Quanten zu erreichen Gravitationseffekte, Sie müssten so viel Energie in eine so kleine Region des Weltraums stecken, dass sie in ein Schwarzes Loch fallen würde, und somit wären Sie angeblich sowieso nicht in der Lage, Informationen aus dem Prozess herauszuholen.

Dies ist eine aktive Forschungssache und überhaupt nicht gut verstanden, würde ich sagen. Es ist jedoch eine interessante Parallele zu Gödels Theoremen, jedoch mit einer physikalischeren Wendung: Das Argument sagt nichts darüber aus, wie viel wir aus der Analyse ihrer mathematischen Struktur über Physik lernen können, sondern wie viel wir daraus vielleicht noch mehr lernen können Grundprinzip der Physik: Experimente machen!

In der gesamten Physik werden Beobachtungen in Bezug auf Mathematik modelliert.Es könnte sich also herausstellen, dass ein Satz in der Realität nicht beweisbar ist, weil Godel unvollständig ist.Und das könnte eine vernünftige physikalische Erklärung haben.Aber es gibt im Moment zumindest keine solche Theorie, AFAIK.

Gödels Theorem erfordert eine geschriebene Sprache (zum Beispiel Englisch), eine Arithmetik einschließlich Primzahlen und einige Axiome, aus denen Sie ableiten möchten, ob Sätze in der Sprache wahr oder falsch sind. Gödel schrieb einen Satz, der nicht als wahr oder falsch erwiesen werden konnte.

Die Physik scheint Gödels Anforderungen zu erfüllen. Wir schreiben Sätze in einer Sprache, verwenden Arithmetik mit Primzahlen und haben Axiome, aus denen wir Sätze über das Ergebnis von Messungen als wahr oder falsch ableiten.

Zunächst könnte man den Schluss ziehen, dass die Physik niemals vollständig sein wird. Es wird einen Satz geben, den wir aus den Axiomen nicht beweisen können, aber wir können mit unseren Instrumenten eine Messung durchführen, um seine Wahrhaftigkeit zu bestimmen. Daher müssen wir noch weitere Axiome hinzufügen, um die Messung vorherzusagen ... Die Physik ist niemals vollständig.

Wir haben jedoch bereits in unseren Theorien angegeben, dass einige Sätze nicht aus den Axiomen oder durch Messung beantwortet werden können. Zum Beispiel ist "Die Phase der Elektronenwellenfunktion um das Wasserstoffatom bei einem bestimmten (x, y, z, t) ist $ \ pi $ radian" wahr oder falsch? .... eine Frage, die wir bestätigen, kann nicht durch Messung beantwortet werden.

Vielleicht wird die Physik eines Tages einen vollständigen Satz von Axiomen haben, und die unbeantwortbaren Gödel-Fragen werden genau die sein, die laut Theorie die Messung nicht beantworten kann.