Dies ist keine wirkliche Antwort auf Ihre Frage, im Wesentlichen, weil Ihr Beitrag keine ( derzeit) Frage enthält, aber für einen Kommentar zu lang ist.

Ihre Aussage, dass

eine Koordinatentransformation eine lineare Abbildung von einem Vektor auf sich selbst mit einer Änderung der Basis ist.

ist durcheinander und letztendlich falsch. Nehmen Sie einen Vektorraum $ V $ und zwei Basen $ \ beta $ und $ \ gamma $ für $ V $. Jede dieser Basen kann verwendet werden, um eine Repräsentationskarte $ r_ \ beta: \ mathbb R ^ n \ zu V $ zu erstellen, die durch $$ r_ \ beta (v) = \ sum_ {j = 1} ^ nv_j e_j $$ gegeben ist wenn $ v = (v_1, \ ldots, v_n) $ und $ \ beta = \ {e_1, \ ldots, e_n \} $. Die Koordinatentransformation ist keine lineare Abbildung von $ V $ zu sich selbst. Stattdessen ist es die Karte $$ r_ \ gamma ^ {- 1} \ circ r_ \ beta: \ mathbb R ^ n \ zu \ mathbb R ^ n, \ tag 1 $$ und nimmt Koordinaten zu Koordinaten.

Um auf den Punkt Ihrer Verwirrung zu kommen, sollte betont werden, dass Covektoren keine Mitglieder von $ V $ sind. Daher gelten die Darstellungskarten in keiner Weise direkt für sie. Stattdessen gehören sie zum dualen Raum $ V ^ \ ast $, mit dem Sie hoffentlich vertraut sind. (Im Allgemeinen würde ich Sie dringend davon abhalten, Texte zu lesen, die vorgeben, das Gesetz zur Unterscheidung zwischen Vektoren und Covektoren festzulegen, ohne ausführlich über den dualen Raum zu sprechen.)

Der duale Raum ist der Vektorraum aller linearen Funktionen von $ V $ in sein Skalarfeld: $$ V = \ {\ varphi: V \ bis \ mathbb R: \ varphi \ text {ist linear} \}. $$ Dies hat dieselbe Dimension wie $ V. $, und jede Basis $ \ beta $ hat eine eindeutige doppelte Basis $ \ beta ^ * = \ {\ varphi_1, \ ldots, \ varphi_n \} $, gekennzeichnet durch $ \ varphi_i (e_j) = \ delta_ {ij} $. Da es sich um eine andere Basis als $ \ beta $ handelt, ist es nicht überraschend, dass die entsprechende Darstellungskarte unterschiedlich ist.

Um die Darstellungskarte in den Raum mit zwei Vektoren zu heben, muss der Begriff neben einer linearen Karte verwendet werden. Es gibt im Allgemeinen keine Möglichkeit, eine lineare Karte $ L: V \ nach W $ zu einer Karte von $ V ^ * $ nach $ W ^ * $ zu heben. Stattdessen muss man den Pfeil umkehren. Bei einer solchen Abbildung, einem funktionalen $ f \ in W ^ * $ und einem Vektor $ v \ in V $ gibt es nur eine sinnvolle Kombination, nämlich $ f (L (v)) $. Das Mapping $$ v \ mapsto f (L (v)) $$ ist ein lineares Mapping von $ V $ in $ \ mathbb R $ und daher in $ V ^ * $. Es wird mit $ L ^ * (f) $ bezeichnet und definiert die Aktion des adjungierten $$ L ^ *: W ^ * \ zu V ^ *. $$

Wenn Sie dies auf das anwenden Repräsentationskarten auf $ V $ erhalten Sie die Adjunkte $ r_ \ beta ^ *: V ^ * \ zu \ mathbb R ^ {n, *} $, wobei letzteres kanonisch $ \ mathbb R ^ n $ entspricht, weil es hat eine kanonische Basis. Die Umkehrung dieser Karte, $ (r_ \ beta ^ *) ^ {- 1} $, ist die Repräsentationskarte $ r _ {\ beta ^ *}: \ mathbb R ^ n \ cong \ mathbb R ^ {n, *} \ bis V ^ * $. Dies ist der Ursprung der 'inversen Transponierungs'-Regel zum Transformieren von Covektoren.

Um die Transformationsregel für Covektoren zwischen zwei Basen zu erhalten, müssen Sie zwei davon aneinander reihen: $$ \ left ((r_ \) gamma ^ *) ^ {- 1} \ right) ^ {- 1} \ circ (r_ \ beta ^ *) ^ {- 1} = r_ \ gamma ^ * \ circ (r_ \ beta ^ *) ^ {- 1 }: \ mathbb R ^ n \ bis \ mathbb R ^ n, $$, was sich sehr von dem für Vektoren unterscheidet, (1).

Denken Sie immer noch, dass Vektoren und Covektoren dasselbe sind?

Nachtrag

Lassen Sie mich abschließend ein weiteres Missverständnis in Ihrer Frage ansprechen:

Ein inneres Produkt befindet sich zwischen Elementen desselben Vektorraums und nicht zwischen zwei Vektorräumen, es ist nicht so, wie es definiert ist.

Innere Produkte werden tatsächlich definiert, indem beide Eingaben aus demselben Vektorraum entnommen werden. Trotzdem ist es immer noch durchaus möglich, eine bilineare Form $ \ langle \ cdot, \ cdot \ rangle zu definieren: V ^ * \ times V \ to \ mathbb R $, die einen Covektor und einen Vektor benötigt, um einen Skalar zu ergeben; es ist einfach die Aktion des ersteren auf das letztere: $$ \ langle \ varphi, v \ rangle = \ varphi (v). $$ Diese bilineare Form ist immer garantiert und setzt eine streng weniger Struktur als ein inneres Produkt voraus. Dies ist das 'innere Produkt', das in Einstein-Notation $ \ varphi_j v ^ j $ lautet.

Dies bezieht sich natürlich auf die innere Produktstruktur $ \ langle \ cdot, \ cdot \ rangle_ \ text {I.P.} $ auf $ V $, wenn es eine gibt. Eine solche Struktur ermöglicht es, Vektoren und Covektoren auf kanonische Weise zu identifizieren: Wenn ein Vektor $ v $ in $ V $ gegeben ist, ist sein entsprechender Covektor die lineare Funktion $$ \ begin {align} i (v) = \ langle v, \ cdot \ rangle_ \ text {IP}: V& \ longrightarrow \ mathbb R \\ w& \ mapsto \ langle v, w \ rangle_ \ text {IP}. \ end {align} $$ Konstruktionsbedingt sind beide bilinearen Formen kanonisch verwandt , so dass das 'innere Produkt' $ \ langle \ cdot, \ cdot \ rangle $ zwischen $ v \ in V ^ * $ und $ w \ in V $ genau das gleiche ist wie das innere Produkt $ \ langle \ cdot, \ cdot \ rangle_ \ text {IP} $ zwischen $ i (v) \ in V $ und $ w \ in V $. Dieser Sprachgebrauch ist vollkommen gerechtfertigt.

Anhang 2 zu Ihrer Frage zum Gradienten.

Ich sollte wirklich versuchen, Sie an dieser Stelle davon zu überzeugen, dass die Transformationsgesetze gelten in der Tat genug, um etwas zu zeigen, ist ein Covector. (Das Argument lautet, dass man eine lineare Funktion auf $ V $ über das von den Komponenten angegebene Formular in $ \ mathbb R ^ {n *} $ definieren kann und die Transformationsgesetze sicherstellen, dass dieses Formular in $ V ^ * $ ist unabhängig von der Basis; alternativ geben die Darstellungskarten angesichts der Komponenten $ f_ \ beta, f_ \ gamma \ in \ mathbb R ^ n $ in Bezug auf zwei Basen die Formen $ r _ {\ beta ^ *} (f_) an \ beta) = r _ {\ gamma ^ *} (f_ \ gamma) \ in V ^ * $, und die beiden sind aufgrund der Transformationsgesetze gleich.)

Es gibt jedoch tatsächlich einen tieferen Grund für die Tatsache, dass der Gradient ein Covektor ist. Im Wesentlichen hat dies damit zu tun, dass die Gleichung $$ df = \ nabla f \ cdot dx $$ eigentlich kein Punktprodukt benötigt; Stattdessen basiert es auf der einfacheren Struktur der bilinearen Dual-Primal-Form $ \ langle \ cdot, \ cdot \ rangle $.

Um dies zu präzisieren, betrachten Sie eine beliebige Funktion $ T: \ mathbb R ^ n \ bis \ mathbb R ^ m $. Die Ableitung von $ T $ bei $ x_0 $ ist definiert als die (eindeutige) lineare Abbildung $ dT_ {x_0}: \ mathbb R ^ n \ zu \ mathbb R ^ m $, so dass $$ T (x) = T ( x_0) + dT_ {x_0} (x-x_0) + O (| x-x_0 | ^ 2), $$ falls vorhanden. Der Gradient ist genau diese Karte; Es wurde als lineares Funktional geboren, dessen Koordinaten über jede Basis $ \ frac {\ partielle f} {\ partielle x_j} $ sind, um sicherzustellen, dass die mehrdimensionale Kette Regel, $$ df = \ sum_j \ frac {\ teilweise f} {\ teilweise x_j} d x_j, $$ ist erfüllt. Um Studenten, die noch nicht mit 1D-Kalkül vertraut sind, das Verständnis zu erleichtern, wird diese lineare Karte meistens als entsprechender Vektor "verkleidet", der durch die euklidische Struktur eindeutig erhältlich ist und dessen Wirkung daher durch diesen euklidischen zurückgehen muss Struktur, um zum ursprünglichen $ df $ zu gelangen.

Anhang 3.

OK, es ist jetzt irgendwie klar, was die Hauptfrage ist (es sei denn, das ändert sich erneut). obwohl es immer noch im Fragentext nicht besonders klar ist. Das, was adressiert werden muss, ist in der Antwort des OP in diesem Thread angegeben:

Der duale Vektorraum ist selbst ein Vektorraum, und die Tatsache, dass er als Zeilenmatrix abgelegt werden muss, basiert darüber, wie wir lineare Karten berechnen und nicht darüber, was lineare Karten tatsächlich sind. Wenn ich die Matrixmultiplikation anders definiert hätte, wäre dies nicht geschehen.

Ich werde auch diese Frage ansprechen: vorausgesetzt, der duale (/ cotangent) Raum ist auch Was zwingt uns, einen Vektorraum so weit vom Ursprünglichen zu unterscheiden, dass wir ihn als Zeilenvektoren anstelle von Spalten anzeigen und sagen, dass seine Transformationsgesetze unterschiedlich sind?

Der Hauptgrund dafür wird von Christoph in seiner Antwort gut angesprochen, aber ich werde darauf näher eingehen. Die Vorstellung, dass etwas Co- oder Contra-Variante ist, ist im Vakuum nicht gut definiert. Wörtlich bedeuten die Begriffe "variiert mit" und "variiert gegen" und sie sind bedeutungslos, es sei denn, man sagt , was das betreffende Objekt mit oder gegen variiert.

Bei der linearen Algebra beginnt man mit einem gegebenen Vektorraum, $ V $. Die nicht angegebene Referenz ist immer die Basis von $ V $: Kovariante Objekte transformieren sich genau wie die Basis, und kontravariante Objekte verwenden die Transponierungsumkehrung der Koeffizientenmatrix der Basistransformation.

Man kann, von Drehen Sie natürlich den Spieß um und konzentrieren Sie sich auf das Duale, $ W = V ^ * $. In diesem Fall wird das ursprüngliche $ V $ jetzt zum Dualen, $ W ^ * = V ^ {**} \ cong V $ . In diesem Fall transformieren sich Größen, die früher mit der Urbasis transformiert wurden, jetzt gegen die Doppelbasis und umgekehrt. Genau deshalb nennen wir es das Duale: Es gibt eine vollständige Dualität zwischen den beiden Räumen.

Wie überall in der Mathematik, wo zwei vollständig duale Räume berücksichtigt werden ( Beispiel, Beispiel, Beispiel , Beispiel, Beispiel) muss man diese Symmetrie brechen, um irgendwohin zu gelangen. Es gibt zwei Klassen von Objekten, die sich unterschiedlich verhalten, und eine Transformation, die die beiden vertauscht. Dies hat zwei unterschiedliche, verwandte Vorteile:

• Alles, was man für eine Gruppe von Objekten beweist, hat eine doppelte Tatsache, die automatisch bewiesen wird.
• Daher muss man immer nur eine beweisen Version der Anweisung.

Wenn man Vektortransformationsgesetze betrachtet, hat (oder kann oder sollte) man immer im Hinterkopf die Tatsache, dass man die Sprache in Bezug auf die dualitätstransformierten Objekte umformulieren kann. Da jedoch der Inhalt der Anweisungen durch die Umwandlung nicht geändert wird, ist es normalerweise nicht sinnvoll, die Umwandlung durchzuführen: Man muss eine -Version angeben, und es gibt keine wirklich Jeder Punkt, an dem beides angegeben wird. Somit bricht einer (willkürlich -ish) die Symmetrie, rollt mit dieser Version und ist sich bewusst, dass eine duale Version der gesamten Entwicklung ebenfalls möglich ist.

Diese duale Version ist jedoch nicht das gleiche. Covektoren können in der Tat als Zeilenvektoren in Bezug auf eine Basis von Covektoren ausgedrückt werden, und die Koeffizienten von Vektoren in $ V $ würden dann mit der neuen Basis anstatt gegen variieren, aber dann würden für jede tatsächliche Implementierung die Matrizen, die Sie verwenden würden Natürlich wird die Dualität transformiert. Sie hätten die Sprache geändert, aber nicht den Inhalt.

Schließlich ist zu beachten, dass die beiden Objekte zwar gleichwertig sind, jedoch nicht gleich sind. Deshalb nennen wir sie dual, anstatt einfach zu sagen, dass sie gleich sind! In Bezug auf Vektorräume muss man also noch beweisen, dass $ V $ und $ V ^ * $ nicht nur doppelt verwandt, sondern auch unterschiedlich sind. Dies wird in der Aussage präzisiert, dass es keinen natürlichen Isomorphismus zwischen einem Vektorraum und seinem dualen gibt, der in der Sprache der Kategorietheorie formuliert und bewiesen ist. Der Begriff des "natürlichen" Isomorphismus ist schwierig, würde aber Folgendes implizieren:

Für jeden Vektorraum $ V $ hätten Sie einen Isomorphismus $ \ sigma_V: V \ zu V ^ * $. Sie möchten, dass dieser Isomorphismus gut mit der Dualitätsstruktur und insbesondere mit den Dualen linearer Transformationen, d. H. Ihren Adjunkten, zusammenspielt. Das bedeutet, dass Sie für alle Vektorräume $ V, W \ in \ mathrm {Vect} $ und jede lineare Transformation $ T: V \ zu W $ das Diagramm

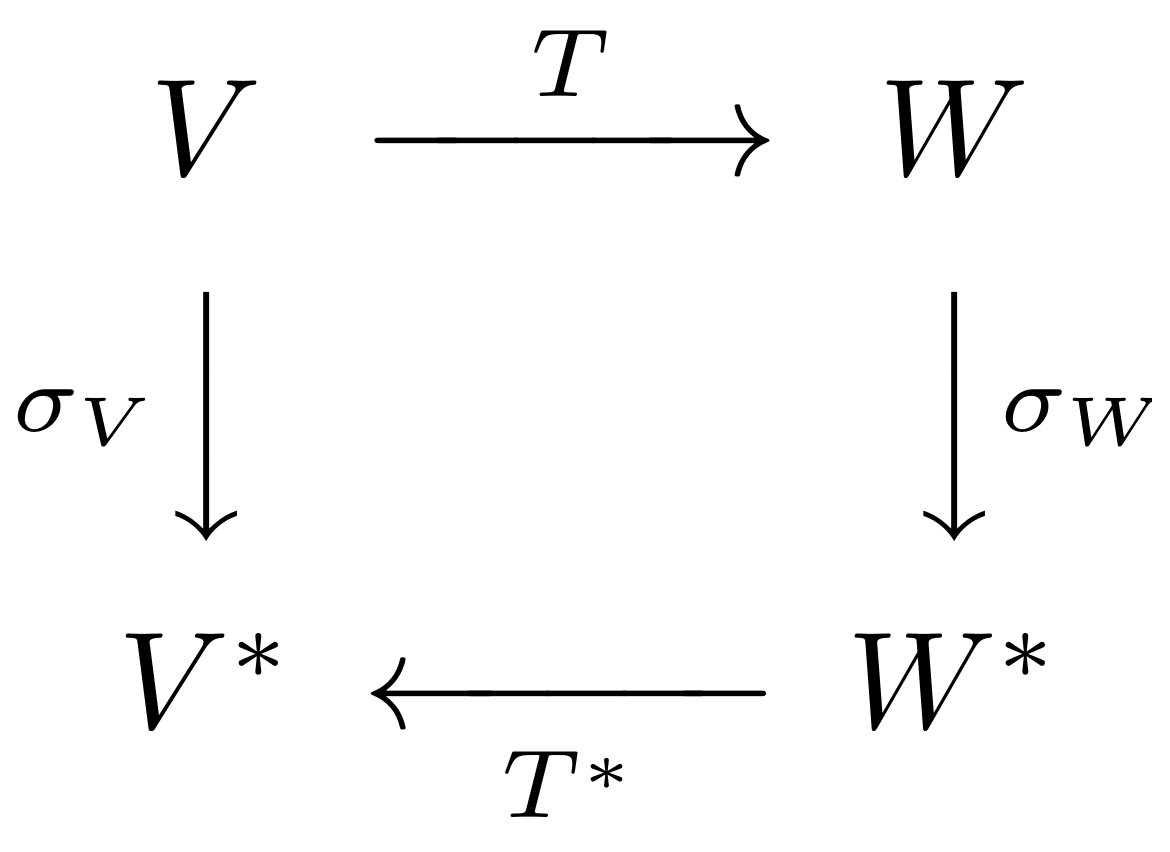p möchten >

pendeln. Das heißt, Sie möchten, dass $ T ^ * \ circ \ sigma_W \ circ T $ gleich $ T $ ist.

Dies ist nachweislich nicht konsistent möglich. Der Grund dafür ist, dass wenn $ V = W $ und $ T $ ein Isomorphismus ist, $ T $ und $ T ^ * $ unterschiedlich sind, aber für ein einfaches Gegenbeispiel können Sie einfach ein reales Vielfaches der Identität nehmen als $ T $. Dies ist genau die formale Aussage der Intuition in garyps großartiger Antwort.

In Apfel-Birnen-Sprachen bedeutet dies, dass ein allgemeiner Vektorraum $ V $ und sein dual $ V ^ * $ sind nicht nur dual (in dem Sinne, dass es eine Transformation gibt, die sie umschaltet und bei zweimaliger Anwendung zurücksetzt), sondern sie unterscheiden sich auch (in dem Sinne, dass es keine einheitliche Möglichkeit gibt, sie zu identifizieren). Aus diesem Grund ist die Dualitätssprache gerechtfertigt.

Ich habe ziemlich viel herumgeschlendert, und hoffentlich ist zumindest ein Teil davon hilfreich. Zusammenfassend muss ich jedoch die Tatsache wegnehmen, dass

Nur weil zwei Objekte gleichwertig sind, heißt das nicht, dass sie gleich sind.

Dies ist übrigens auch eine direkte Antwort auf den Fragentitel: Nein, es ist nicht dumm. Sie sind gleichwertig, aber immer noch unterschiedlich.

Wir erwarten, dass sich ein Vektor auf eine bestimmte Weise ändert, wenn wir die Skala ändern, mit der wir die Entfernung messen. Betrachten Sie den Vektor $$ \ vec {x} = (1, 0, 0) \, \ mathrm {m} $$ Wenn wir den Maßstab ändern und jetzt in Zentimetern messen, wird dieser Vektor zu $$ \ vec {x} = (100, 0, 0) \, \ mathrm {cm} $$ Betrachten Sie nun einen Vektor, der eine Kraft darstellt: $$ \ vec {F} = (1,0,0) \, \ mathrm {J / m} $$ wobei I ' Wir haben uns entschieden, J / m für Newton zu schreiben, um uns daran zu erinnern, dass Kraft der Gradient einer möglichen Funktion ist. Nun, dieses Potenzial wird sich nicht ändern, weil ich die Skalen geändert habe. Es sitzt immer noch irgendwo im Weltraum, nur dort. Wie sieht der Kraftvektor aus, wenn er in einem cm-basierten Rahmen gemessen wird? $$ \ vec {F} = (0.01, 0,0) \, \ mathrm {J / cm} $$ Dieser "Vektor" $ \ vec {F} $ transformiert sich nicht richtig! Beachten Sie jedoch, dass in beiden Frames die Berechnung der Arbeit, die durch Bewegen eines Objekts um einen Meter gegen eine Kraft von einem Newton geleistet wird, dieselbe bleibt: $$ W = \ vec {F} \ cdot \ vec {x} = (1,0,0 ) \ cdot (1,0,0) = (100,0,0) \ cdot (0,01, 0,0) = 1 \, \ mathrm {J} $$ Als Gradienten definierte Größen gehören zu einem Vektorraum, aber es ist eine andere Art von Vektorraum als der, der Entfernungen enthält. Daher unterscheiden wir covariant (manchmal als cogradient bezeichnet - "wie ein Gradient" - insbesondere in der älteren Literatur) und contravariant (oder contragradient - "Gegenteil des Gradienten")

Damit die physikalisch wichtige Menge energy unabhängig von dem Rahmen, den wir bewerten, denselben Wert hat in müssen wir erkennen, dass es zwei Arten von Vektoren gibt, und sie müssen bei Änderung der Koordinaten unterschiedlich behandelt werden.

Hier können noch zwei weitere Punkte hervorgehoben werden. Es tut mir leid, wenn ich jemanden wiederhole.

In gewisser Weise haben Sie Recht, dass es keine intrinsische Möglichkeit gibt zu sagen, welcher Raum das Original und welcher der Dual ist, wenn Sie einen Vektorraum und dessen Dual haben. Dies liegt daran, dass es einen kanonischen Isomorphismus zwischen einem Vektorraum und dem Dual seines Dual gibt. Mit anderen Worten, wenn $ V $ ein Vektorraum ist und $ W = V ^ * $ sein Dual ist, dann ist $ W ^ * = (V ^ *) ^ * $ isomorph zu $ ​​V $ (auf kanonische Weise). Daher könnte das Paar $ V $ und $ W $ als ein Vektorraum $ V $ und sein duales $ W $ oder als ein Vektorraum $ W $ und sein duales $ V = W ^ * $ angesehen werden.

Im Kontext einer Mannigfaltigkeit, in der normalerweise die Wörter kontravariante und kovariante Vektoren vorkommen, sagen Sie, dass Sie zuerst den Tangentenraum an einem Punkt und dann den dualen Kotangensraum definieren müssen, bevor Sie über eine Form, Differentiale und sprechen können demnächst. Dies ist jedoch nicht der Fall. Es ist wahr, dass dies in den meisten Büchern der übliche Weg ist, aber nicht der einzig mögliche. Wenn Sie ein Algebraist im Geiste sind, haben Sie möglicherweise die folgende Definition gesehen und bevorzugen sie. Sei $ M $ eine differenzierbare Mannigfaltigkeit und $ p \ in M ​​$ ein Punkt. Betrachten Sie den Ring $ \ mathcal O_p $ von Keimen glatter Funktionen bei $ p $. Es ist ein lokaler Ring, dh er hat ein eindeutiges maximales Ideal $ \ mathcal m_p $, das aus den Keimen von Funktionen besteht, die bei $ p $ verschwinden. Dann ist der Ring $ \ mathcal O_p / \ mathcal m_p $ offensichtlich isomorph zum Feld von reellen Zahlen. Der Quotient $ \ mathcal m_p / \ mathcal m ^ 2_p $ ist auf natürliche Weise ein Vektorraum über $ \ mathcal O_p / \ mathcal m_p = \ mathbb R $. Dies ist der Kotangensraum des Verteilers an diesem Punkt, der normalerweise mit $ T ^ * _ pM $ bezeichnet wird. Auf diese Weise können Sie die „Covektoren“ definieren, ohne zuerst die Vektoren zu definieren. Der Tangentenraum ist dann das Duale.

I) Nein, Es ist wichtig, zwischen kovarianten und kontravarianten Tensoren zu unterscheiden.

OPs Link erwähnt Differentialgeometrie. Wenn man diese Objekte nur im Kontext von pseudo-Riemannschen Mannigfaltigkeiten $ (M; g) $ untersucht hat, die mit einer (invertierbaren) Metrik $ (0,2) $ Tensor $ g $ ausgestattet sind Dann kann die Existenz des musikalischen Isomorphismus möglicherweise die genauen Begriffe von kovarianten und kontravarianten Tensoren in einigen Behandlungen unnötig verschleiern.

Daher wird empfohlen, dies in einer bloßen Umgebung einer Mannigfaltigkeit $ M $ zu untersuchen, ohne zusätzliche Strukturen wie einen metrischen Tensor $ g $ anzunehmen.

II) Wenn man über kovariante und kontravariante Tensoren verwirrt ist, sollte man dies zunächst im Bereich multi-linearer Karten endlicher dimensionaler Vektorräume $ V $ untersuchen (im Gegensatz zum Kontext von Differentialgeometrie und Mannigfaltigkeiten $ M $).

Die obige Empfehlung übersetzt (in der multi-linearen Einstellung) in das Studium multilinearer Karten eines endlichdimensionalen Vektorraums $ V $ ohne unter der Annahme zusätzlicher Strukturen wie eines (nicht entarteten) inneren Produkts $ \ langle \ cdot | \ cdot \ rangle: V \ times V \ to \ mathbb {R} $.

Natürlich gibt es immer unendlich viele Möglichkeiten, ein (nicht entartetes) inneres Produkt $ \ langle \ cdot | zu platzieren \ cdot \ rangle $ auf einem endlichdimensionalen Vektorraum $ V $, von denen jeder zu einem musikalischen Isomorphismus führt: $ V \ cong V ^ * $. Der entscheidende Punkt ist jedoch, dass es keine kanonische Wahl für ein (nicht entartetes) inneres Produkt $ \ langle \ cdot | gibt \ cdot \ rangle $ on $ V $.

Der Begriff der Co- und Kontravarianz hängt vom Kontext ab: Wenn Sie so klar wie möglich sein möchten, sollten Sie tatsächlich erwähnen, was die Komponenten co- oder kontravarianz transformieren.

Im Fall von Das implizite Kontext, das algebraische Dual von endlichdimensionalen Vektorräumen, ist eine Änderung der Basis des Vektorraums. Dann können wir untersuchen, wie sich die Komponenten von Vektoren und Doppelvektoren in Bezug auf diese Änderung verhalten.

Im Fall der Differentialgeometrie ist der implizite Kontext die Änderung der Koordinaten des Basisverteilers, die a induziert Änderung der Basis des durch die Jacobi-Matrix gegebenen Tangentenraums. In Bezug auf diese Änderung der Basis transformieren sich die Komponenten von Tangentenvektoren kontravariant und die Komponenten von Kotangensvektoren kovariant.

An dieser Stelle ist zu erwähnen, dass Tangenten- und Kotangensvektoren unabhängig von ihrer Transformation definiert werden können Gesetze und ohne die Dualitätspaarung zu nutzen: Moralisch gesehen (damit wir das Problem nicht mit technischen Aspekten verwechseln) sind Tangentenvektoren über eine Mannigfaltigkeit $ M $ Äquivalenzklassen von Karten $ \ mathbb R \ zu M $, während Kotangensvektoren dies sind Äquivalenzklassen von Karten $ M \ bis \ mathbb R $. Beide bilden für sich Vektorräume, und jeder kann als algebraisches Dual des anderen betrachtet werden, sobald Sie einen Begriff der Paarung einführen. Es handelt sich jedoch um unterschiedliche geometrische Objekte. Eine Möglichkeit, diese Unterscheidung deutlich zu machen, besteht darin, das Verhalten ihrer Koordinaten zu untersuchen.

Ich werde sagen, dass die Standarddefinition von Vektoren und Einformen nicht die sauberste der Welt ist. Eine moderne Definition von Vektoren würde sagen, dass ein Vektorraum eine Abbildung der Funktionen auf den Raum auf sich selbst ist, die die Leibniz-Regel erfüllt und linear ist (alternativ ist der Vektorraum die lokale lineare Approximation des Raums). Dann ist die Menge der Einformen eine lineare Abbildung vom Vektorraum auf den Funktionsraum im Tangentenraum.

Es gibt Vektoren eines Vektorraums (eine abstrakte mathematische Berechtigung). Dann gibt es für einen Vektorraum entsprechende Doppelräume. Ein Element eines dualen Raums ordnet das Element des Vektorraums $ R $ zu. Diese Zahl wird als $ <a, b> $, das innere Produkt, bezeichnet. Nun haben der duale Raum und der Vektorraum eine Basis, die durch $ <e ^ i, e_j> = \ delta_ {ij} $ verbunden sind. Angenommen, es gibt eine lineare Transformation von $ Av = b $ für den Vektorraum, und A gehört zum dualen Raum und b gehört zu $ ​​R $. Wenn ich mich dann für eine neue Basis für $ v $ entscheide, muss ich eine lineare Transformation auf v anwenden, die eine quadratische Matrix $ B $ ist. Jetzt schreibe ich die Gleichung als $ A $ $ B ^ {- 1} $ $ B $ $ v $ = $ b $. Dies ergibt nun die lineare Transformation $ A $ auf einer neuen Basis, die durch die Matrix $ A $ $ B ^ {- 1} $ gegeben ist, die wiederum eine Zeilenmatrix sein wird. Was nun passiert ist, ist, dass wir die Basis sowohl des Vektorraums als auch seines dualen Raums so geändert haben, dass die Bedingung $ <e ^ i, e_j> = \ delta_ {ij} $ beibehalten wird und aufgrund der Art und Weise, wie sich der duale Vektor in diesem Fall transformiert nannten wir es einen kovarianten Vektor. Diese Benennung ist jedoch nicht universell. Es ist ein relatives Konzept und kann von Situation zu Situation variieren.

da der duale Vektorraum selbst ein Vektorraum ist und die Tatsache, dass er als Zeilenmatrix abgelegt werden muss, davon abhängt, wie wir berechnen lineare Karten und nicht, was lineare Karten tatsächlich sind. Wenn ich die Matrixmultiplikation anders definiert hätte, wäre dies nicht geschehen.

Nun hätte die Basisänderungstransformation, die wir für den dualen Raum erreicht haben, genauso wie der Vektorraum selbst erreicht werden können, wenn wir dargestellt hätten der Doppelvektor als Spaltenvektor und hat die Basisänderung separat herausgefunden, und somit hätte sich der Vektor als $ X $ $ A ^ T $ transformiert, wobei $ A ^ T $ den Doppelvektor als Spaltenvektor bezeichnet.

Nun transformiert sich der duale Vektor wie der kontravariante Vektor selbst unter Basisänderungstransformation.

Die gleiche Transformation kann also auf jede Art und Weise erreicht werden, die Sie als kontravariant oder kovariant mögen. Ein Vektor ist ein Vektor.

Die Co / Contra-Unterscheidung ist nur dann sinnvoll, wenn es um Vektorfelder geht. Selbst dann wird der Unterschied nur sichtbar, wenn es sich um gekrümmte Räume oder zumindest krummlinige Koordinatensysteme handelt. Der Unterschied ergibt sich aus der Beziehung der Vektoren zu dem zugrunde liegenden Raum oder der Mannigfaltigkeit, auf der Die Felder sind definiert. Kontravariante Vektoren sind dann das, was die Leute normalerweise als Vektoren betrachten. Ein Großteil der formalen Maschinerie kann umgangen werden, wenn Sie die Vorstellung eines Skalarfelds auf einer Mannigfaltigkeit als offensichtlich betrachten :). Ein (kontravarianter) Vektor ist dann Dies misst die Änderungsrate eines Skalarfelds a an einem Punkt in einer bestimmten Richtung. Dies wird formalisiert, indem Vektoren als Operatoren auf Skalarfeldern betrachtet werden, die bestimmte Bedingungen erfüllen. Diese Ansicht bewirkt, dass kontravariante Vektorfelder von Skalarfeldern zu Skalarfeldern funktionieren. Kovariante Vektoren (oder Covektoren) wirken dann auf Vektoren, um ihre Komponente in einer bestimmten Richtung zu messen. Dadurch werden Covektorfelderfunktionen von Vektorfeldern zu Skalarfeldern. Dies ist nicht trivial dass wir keine Metriken, Normen, Punktprodukte oder Vorstellungen von Orthogonalität auf den Vektoren oder der zugrunde liegenden Mannigfaltigkeit annehmen. Sobald eine Metrik eingeführt wird, erhalten wir einen natürlichen Isomorphismus zwischen Vektoren und Covektoren, werden dann kovariante und kontravariante Basen verwendet, um die darzustellen Das gleiche geometrische Objekt wie ein Vektor oder ein Covektor. Beachten Sie, dass kontravariante Vektoren in Begriffen oder kovarianten Basen dargestellt werden und umgekehrt.

Wir können nicht sagen, dass die Unterscheidung zwischen Kovariantenvektor und Kovariantenvektor etwas dumm ist.

Es besteht jedoch keine Notwendigkeit, den physikalischen Vektor auf Kovariante oder Kovariante zu beschränken. Tatsächlich kann jeder Vektor, wie z. B. die Geschwindigkeit, der Gradient oder ein anderer Vektortyp, in der Koordinatentransformation entweder als kovariant oder als kontravariant angesehen werden, obwohl Sie möglicherweise feststellen, dass sich die Geschwindigkeit normalerweise auf den kontravarianten Vektor bezieht und auf den Gradienten Bezug genommen wird kovarianter Vektor.

Per Definition gehorchen die Komponenten einer kovarianten Vektortransformation dem Gesetz: $$ \ overline A_i = \ sum_ {j = 1} ^ n \ frac {\ partielle x ^ j} {\ partielle \ overline x ^ i} A_j \ qquad \ qquad (1 ) $$ span>

und die Komponenten einer kontravarianten Vektortransformation gehorchen dem Gesetz: $$ \ overline A ^ i = \ sum_ {j = 1} ^ n \ frac {\ partielle \ overline x ^ j} {\ partielle x ^ i} A ^ j \ qquad \ qquad (2) $$ span>

Es gibt keine Einschränkung für die Vektortypen $ A_j $ span> und $ A ^ j $ span>. und wir können die Koordinatentransformation gemäß den Regeln durchführen.