... wenn eine Linse alle einfallenden Lichtstrahlen so biegt, dass sie sich im Brennpunkt schneiden? Sollte dies nicht einen einzelnen Lichtpunkt erzeugen ...?

(In Ihrem Diagramm befindet sich das Quellbild im Unendlichen. Ich werde die Analyse entlang dieser Idee fortsetzen.) P. >

Es stimmt, dass alle Strahlen parallel zur Achse auf diesen einzelnen Punkt fokussieren. Nicht alle Strahlen sind jedoch parallel zur Achse:

Strahlen, die aus verschiedenen Winkeln kommen, fokussieren auf verschiedene Punkte. So entsteht ein Bild.

Eine konvexe Linse fokussiert nicht alle Strahlen auf einen einzelnen Punkt. Es fokussiert die parallelen Strahlen aller Achsen auf den Brennpunkt. Es fokussiert auch alle Strahlen, die von einem bestimmten Punkt ausgehen, auf einen entsprechenden Punkt auf der anderen Seite. Dieser Punkt ist das Bild des ursprünglichen Punkts.

Das Standarddiagramm zeigt, dass eine Linse alle achsparallelen einfallenden Strahlen zum Brennpunkt sendet. Parallele Strahlen können als von einem Punkt im Unendlichen ausgehend betrachtet werden. Sie können sich den Brennpunkt also als das Bild eines Punktes im Unendlichen vorstellen.

Allgemeinere Strahlendiagramme sehen wie folgt aus: this:

Die vollständigen Regeln zum Zeichnen von Strahlendiagrammen finden Sie in der Hyperphysik-Artikel zum Thema:

1. Ein Strahl von der Oberseite des Objekts, der parallel zur Mittellinie senkrecht zur Linse verläuft. Jenseits der Linse passiert es den Hauptschwerpunkt. Bei einer negativen Linse geht sie von der Linse aus, als ob sie vom Brennpunkt auf der nahen Seite der Linse ausgeht.
2. Ein Strahl durch die Mitte der Linse, der nicht abgelenkt wird. (Tatsächlich wird es auf der nahen Seite der Linse nach unten und auf der Austrittsseite der Linse wieder nach oben bewegt, aber der resultierende leichte Versatz wird bei dünnen Linsen vernachlässigt.)
3. Ein Strahl durch das Prinzip Brennpunkt auf der nahen Seite des Objektivs. Beim Austritt aus der Linse verläuft sie parallel zur Mittellinie. Der dritte Strahl wird nicht wirklich benötigt, da die ersten beiden das Bild lokalisieren.
ol>

Ihr Diagramm zeigt parallele Lichtstrahlen aus dem Unendlichen. Licht, das in der realen Welt in das Auge eintritt, ist nicht alle parallel.

In der realen Welt trifft alles Licht, das von einem einzelnen Punkt reflektiert wird, auf den Sensor (Augenkegel, digitaler Sensor, etc) an einem einzelnen Punkt, vorausgesetzt, dieser Punkt ist im Fokus. Licht von verschiedenen Punkten trifft jedoch an verschiedenen Stellen auf den Sensor und erzeugt das Bild, das Sie sehen.

Wenn der Punkt nicht ist Im Fokus wird es in einem Kreis auf dem Sensor verteilt. Fotografen nennen dies den Kreis der Verwirrung.

Mit diesem Tool herumspielen sollte es ziemlich offensichtlich machen. Ich habe diese Bilder aus meiner Antwort auf die Frage Photography.SE übernommen. Wie funktioniert die Blende, ohne das auf den Sensor treffende Bild zu „beschneiden“?

Um ehrlich zu sein: Die geometrische Optik ist falsch. Es reicht für kleine Winkel und nicht zu komplizierte Einstellungen aus, ist aber dennoch eine Annäherung.

Das erste: Normale Objektive haben keinen Brennpunkt, sondern etwas, das eher einer Linie ähnelt, das sogenannte Ätzmittel. Die richtige Form, um einen perfekten Punkt auf der Linie zu erhalten, die die Mitte der Linse kreuzt (ich nenne das jetzt Achse ), ist keine sphärische Form, sondern eine komplizierte Kurve, das kartesische Ovoid. Sie erhalten also überhaupt kein Punktbild von normalen optischen Oberflächen. Es gibt aplanatische Linsen , aber sie sind extrem teuer.

Zweitens: Selbst wenn Sie eine aplanatische Linse haben, ist Licht kein Strahl, sondern eine Wellenfront. Eine perfekte planare Wellenfront, die eine aplanatische Linse passiert, bildet immer noch keinen Punkt, sondern eine sogenannte luftige Scheibe. Sie sehen das sehr gut, wenn Sie die Vergrößerung erhöhen; Irgendwann wird das Bild immer unscharfer, die luftigen Scheiben der Punktbilder beginnen sich zu überlappen und das Bild zu ruinieren. Die einzige Möglichkeit, dies zu vermeiden, besteht darin, die Linse oder den Spiegel zu vergrößern, wodurch die luftige Scheibe kleiner wird (aus diesem Grund benötigen Astronomen große, große Linsen und Spiegel).

Aber selbst das reicht nicht aus genug, wenn Sie wirklich hohe Qualität wünschen, in diesem Fall benötigen Sie die genauen Lichtgleichungen, die durch die Maxwell-Gleichungen beschrieben werden.

Jetzt brauchen wir ein Bild, ich verwende die Open-Source-Bild der deutschen Wikipedia unter "Linsengleichung":

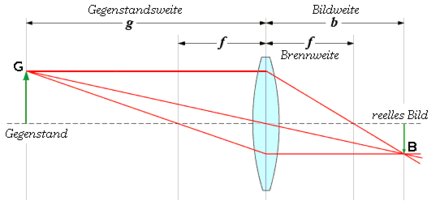
Wie Sie sehen, befinden sich die Strahlen in der Nähe der Linse, wenn sich die Quelle der Lichtstrahlen befindet laufen nicht parallel und ihr Bild entwickelt sich nicht im Brennpunkt f, sondern in größerer Entfernung. Sie verwenden zwei Strahlen vom selben Punkt: einen parallel zur Achse, die den Brennpunkt kreuzt, und einen, der vom Punkt genau durch die Linse verläuft. Wo sie sich kreuzen, ist das Bild des Quellpunkts und dies ist nicht der Brennpunkt!

Ihre Frage enthält einen Irrtum, der Ihre Verwirrung stiften könnte. Es ist nicht alles Licht , das auf einen Punkt fokussiert wird, sondern nur Strahlen parallel zur Linsenachse!
Für den Fall von zwei (Punktquellen-) Sternen gilt: Wenn die Strahlen eines Sterns parallel zur Linsenachse sind, sind die Strahlen des anderen Sterns nicht (nicht kolinear), daher erscheint sein Bild an einem anderen Punkt als der erste Stern.