Ja, Logarithmen geben immer dimensionslose Zahlen an, aber nein, es ist nicht physikalisch, den Logarithmus von irgendetwas mit Einheiten zu nehmen.

Stattdessen gibt es immer eine Standardeinheit. In Ihrem Beispiel ist der Standard der Kilometer. Dann werden 20 km unter der Protokolltransformation zu $ ​​\ ln (20 \; \ textrm {km} \; / \; \ textrm {km} \;) $. In ähnlicher Weise ist das Protokoll von 10 cm mit dieser Skala
$$ \ ln (10 \; \ textrm {cm} \; / 10 \; \ textrm {km} \;) = \ ln (10 \ mal 10) ^ {- 3} / 10 ^ {3}) = \ ln (10 ^ {- 5}) $$

Hier ist eine "mathematische", aber höchst unphysische Antwort.

Mit diesem $ km \ cdot km = (km) ^ 2 $ usw. können wir die Arithmetik von Zahlen formal definieren mit Einheiten über einer abgestuften Algebra $ A = \ oplus_ {k \ in \ mathbb {N}} V_k $ wobei $ V_k = \ otimes ^ k V $ wobei $ V $ als Eins behandelt wird- dimensionaler realer Vektorraum ($ V_0 $ ist der Skalar $ \ mathbb {R} $). Die Wahl der Einheit ist die Wahl eines Basisvektors in $ V $. $ V_0 $ ist der reine Skalar. Für jede Auswahl eines Basisvektors $ v \ in V $ erhalten wir eine Zuordnung von der unendlichen Folge $ \ mathbb {R} ^ {\ mathbb {N}} \ zu A $, wobei diese Folge über $ (r_k) \ to realisiert wird [r_k] _v = \ sum r_k (\ otimes ^ kv) $. Wir definieren wie gewohnt die Multiplikation $ V_k \ times V_ {k '} \ mit V_ {k + k'} $.

(Wir werden die negativen Leistungseinheiten vorerst nicht definieren. Aber sie können wahrscheinlich analog eingebaut werden.)

Dann können wir formal $ \ exp: A \ bis A $ definieren durch die Potenzreihenerweiterung

$$ \ exp a = \ sum_ {k = 0} ^ {\ infty} \ frac {1} {k!} a ^ k $$

wobei $ a ^ k $ im Sinne der abgestuften Algebra definiert ist. Und dort haben wir definiert, was es für $ \ exp $ von etwas mit Einheiten bedeutet. Die Änderung der Basis von $ \ exp $ wird von $ y ^ a = \ exp (\ ln (y) \ cdot a) $ behandelt. In ähnlicher Weise wird die Änderung von Einheiten natürlich berücksichtigt, indem eine Änderung der Basis auf einem eindimensionalen realen Vektorraum nur eine Multiplikation mit Skalaren ist. Mit anderen Worten, wir haben $ [r_k] _v = [r'_k] _ {v '} $ wobei $ r_k = s ^ kr'_k $ wenn $ v = s v' $.

Damit können wir die Potenzreihenerweiterung formal invertieren, um herauszufinden, was $ \ ln $ "sein sollte". Repariere eine Einheit $ v $. Nehmen Sie $ (r_k) \ in \ mathbb {R} ^ {\ mathbb {N}} $ und betrachten Sie $ [r_k] _v \ in A $. Um $ \ ln [r_k] _v $ zu finden, müssen wir $ (s_k) \ in \ mathbb {R} ^ {\ mathbb {N}} $ so finden, dass

$$ \ begin {align} r_0 & = \ exp s_0 \\ r_1 & = e ^ {s_0} s_1 \\ r_2 & = e ^ {s_0} (s_2 + \ frac {1} {2} s_1 ^ 2) \\ & \ vdots \ vdots \ { ausrichten} $$

(Wir können auch die Taylor-Erweiterung von $ \ ln $ um $ 1 \ in \ mathbb {R} $ verwenden, um den Ausdruck für $ (s_k) $ in Bezug auf $ (r_k) $ zu erhalten.)

Leider ist $ \ ln 1 km $ auch in diesem Rahmen noch nicht genau definiert: Im Bild von $ \ exp $ ist $ r_0 $ notwendigerweise positiv. Formal ist es möglich, $ \ ln (1 km) = \ ln (1 + (1 km - 1)) $ als die ziemlich divergierende Potenzreihe

$$ \ ln (1 m) zu definieren. = \ sum \ frac {(- 1) ^ {k + 1}} {k} (-1 + 1 (m)) ^ k = \ sum \ frac {-1} {k} + \ sum 1 (m) - \ sum \ frac {k-1} {2} (m ^ 2) + \ cdots $$

Nun ein bisschen Spaß mit abweichenden Serien: Beachten Sie, dass $ \ sum 1 = \ sum (-1) ^ k (-1) ^ k = \ sum (-1) ^ kx ^ k | _ {- 1} $ ist die Taylor-Reihenerweiterung von $ 1 / x $ um $ x_0 = 1 $, die mit $ -1 $ bewertet wird Der zweite Term ist nominell $ \ lim_ {x \ bis 0+} 1 / x $. Selbst wenn wir regulieren:

$$ \ lim _ {\ delta \ bis 0+} \ ln (\ delta + 1m) = \ lim _ {\ delta \ bis 0+} \ ln \ delta + \ Delta ^ {- 1} m + \ cdots $$

ist immer noch stark divergent.

(Beachten Sie, dass jedoch $ \ ln (1 + 1 km) = \ sum (-1) ^ {j + 1} / j (km) ^ j $ als formale Kraft gut definiert ist Serie.)

Worum ging es in diesem Beitrag? Dieser Beitrag wird hauptsächlich mit der Schlussfolgerung behandelt, dass $ \ log m $ eine "dimensionslose Zahl" ist, wie in der Erklärung der Frage angegeben. Während wir in der üblichen Arithmetik lernen, dass wir Orangen keine Äpfel hinzufügen können, ist dies nur dann der Fall, wenn wir versuchen, ein Objekt im $ \ mathbb {Z} $ - Modul von Äpfeln zu einem separaten Objekt in hinzuzufügen das $ \ mathbb {Z} $ - Orangenmodul. Wenn Sie bereit sind, im Direktsummenmodul von Äpfeln $ \ oplus $ Orangen zu arbeiten, können Sie tatsächlich Äpfel zu Orangen hinzufügen.

Um implizit zu behaupten, dass $ \ log $ für Objekte mit Einheiten sinnvoll ist (und in ähnlicher Weise, dass $ \ exp $ für Objekte von Einheiten sinnvoll ist), müssen wir bereits in einem System arbeiten, dem der benotete $ \ mathbb {R} $ - Algebra, in der Sie einem Vektor (ein Objekt mit Einheiten) einen Skalar (ein Objekt ohne Einheiten) hinzufügen können. Wenn Sie also behaupten, dass Sie $ \ log km $ verstehen möchten, können Sie daraus nicht schließen, dass $ 3 $ und $ \ log m $ dieselben Einheiten haben müssen.

Das ist eine lustige Frage. Es fällt mir schwer, die Transformation $ ln $ in den Griff zu bekommen, daher schreibe ich Dinge in Exponenten.

$$ \ mathrm {value} = \ ln (10 \ \ mathrm {km}) $$$$ e ^ {\ mathrm {value}} = 10 \ \ mathrm {km} $$

Die Zahl $ e $ ist natürlich ohne Einheit. Was sind die zulässigen Einheiten der Potenz, wenn ich eine Zahl zu einer Potenz erhöhe? Wenn ich $ x ^ 2 $ schreibe, gehe ich intuitiv davon aus, dass $ 2 $ keine Einheiten hat, da es sich nur um eine Zählung handelt, mit der $ x \ times x = x ^ 2 $ ausgedrückt wird.

Also Ich habe mich von Carls Antwort überzeugt, und ich würde einen Logarithmus benötigen, um eine Referenz zu haben, die Sinn ergibt. Zum Beispiel:

$$ e ^ {\ mathrm {value}} = \ frac {10 \ \ mathrm {km}} {1 \ \ mathrm {km}} $$

Die vorherige Alternative von $ e $, die auf eine Potenz angehoben wird, die einer physikalischen Größe mit realen Einheiten entspricht, scheint das perfekte Beispiel für etwas Unsinniges zu sein.

Protokolldiagramme

Ich habe eine andere Frage, die sich aus Ihrer Frage ergibt, und ich werde versuchen, sie hier zu beantworten. Ich erinnere mich besonders an die Ableitung von Log-Log- und Linear-Log-Plots in Ingenieurklassen. Wir hatten eine Rechtfertigung dafür, aber es scheint an der Oberfläche unsinnig zu sein, also lasst uns eintauchen. Hier ist ein Beispiel für ein Log-Log-Diagramm. Ich zeige das Diagramm und biete dann eine Gleichung für die dargestellte Linie an.

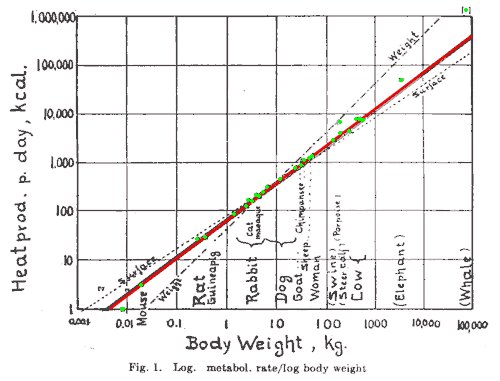
^{Bildquelle: Wikipedia sup>}

Ich beginne, Dinge aus der Grundform $ y = mx + b $ zu schreiben, und ändere sie dann nach Bedarf. Da ich eine beliebige Konstante verwende, werde ich sie bei Bedarf verfälschen.

$$ \ log (p) = a \ log (m) + b = a (\ log (m) + b ') = a \ log (b' 'm) = \ log (b' '^ am ^ a) = \ log \ bigg (\ frac {p_0} {m_0 ^ a} m ^ a \ bigg) $$$$ p = p_0 \ left (\ frac {m} {m_0} \ right) ^ a $$

Wie Magie kommt eine erkennbare Form durch. Das Beobachten einer linearen Beziehung in einem Log-Log-Diagramm bedeutet wirklich, dass Sie eine Potenzanpassung beobachten, keine lineare Anpassung. Ein Schüler kann immer noch fragen "aber was sind a und b", was etwas schwieriger ist. Erstens habe ich $ a $ nicht manipuliert, sodass Sie die Bedeutung direkt aus der endgültigen Form übernehmen können, das heißt, es ist ein Exponent und somit einheitlos. Für b gilt:

$$ b = ab '= a \ log (b' ') = a \ log \ bigg (\ frac {p_0 ^ {1 / a}} {m_0} \ bigg) = \ log \ left (\ frac {p_0} {m_0 ^ a} \ right) $$

Dies zeigt, dass $ b $ ebenfalls ohne Einheit ist, aber es gibt auch eine Interpretation für $ p_0 $, das ist das Referenz-y-Wert bei einem Referenz-x-Wert ($ m_0 $). Ich gehe zum linearen Log-Plot oder einer Semi-Log-Skala über.

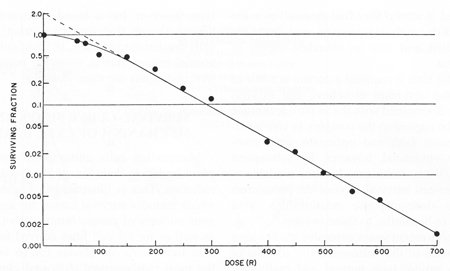
^{Bildquelle: J. Exp. Med. 103 , 653 (1956). sup>}

Ich bezeichne $ f $ für "überlebende Fraktion" und $ d $ für Dosis. Die Gleichung für eine Regression, die im obigen Diagramm linear erscheint, lautet wie folgt:

$$ \ log (f) = ad + b $$$$ f = e ^ {ad + b} = e ^ be ^ {ad} = f_0 e ^ {ad} $$

Es ist wichtig anzumerken, dass $ b $ die ganze Zeit über zweifelhafte Einheiten hatte, genau wie im Fall von Log-Log, aber das tut es nicht. Es ist nicht wirklich wichtig, weil eine nützlichere Form natürlich aus der Mathematik kommt. Der Wert $ f_0 $ wäre der Basiswert (in diesem Fall 100%) bei $ d = 0 $.

Zusammenfassung: Die Annahme einer linearen Beziehung in Protokolldiagrammen setzt tatsächlich voraus, dass die tatsächliche Beziehung einigen folgt nichtlineare Form, und die Einheiten funktionieren, sobald Sie die Mathematik durchgeführt haben, aber die Interpretation der Werte kann nicht trivial sein.

Es ist etwas, das weder eine physikalische Größe noch eine dimensionslose Zahl ist, sondern etwas, das nur als Logarithmus einer physikalischen Größe beschrieben werden kann. Dies ist kein großes Problem: Sei $ \ mathcal {P} $ der Raum der physikalischen Größen. Wir können diesen Raum vektorraumartig durch basenphysikalische Einheiten (z. B. SI) überspannen, wie von Willie Wong beschrieben. Was wichtig ist: Wir wissen, dass wir in diesem Raum bestimmte Operationen nicht ausführen können, zum Beispiel können wir einem elektrischen Strom keine Masse hinzufügen. Das Hinzufügen von Mengen $ a, b \ in \ mathcal {P} $ wird nur definiert, wenn $ a $ und $ b $ dieselbe Dimension haben, dh wenn $ \ x \ in \ mathbb {R} $ existiert, so dass $ a = xb $. Die Multiplikation ist immer definiert und ergibt immer wieder eine physikalische Größe. (Dies definiert auch Potenzen physikalischer Größen, aber nicht das Exponential einer von ihnen.)
Wir wissen dann, dass $ \ mathbb {R} \ subset \ mathcal {P} $, da zum Beispiel Bei zwei Längen $ a, b \ in \ mathcal {P} $ ist das Verhältnis $ \ tfrac {a} b $ eine dimensionslose Zahl. Für diese dimensionslosen Größen wird der Logarithmus von Anfang an definiert.

Es ist ganz einfach, ihn auf einen vollen Raum zu erweitern $ \ ln \! \! \ Mathcal {P} \ supset \ mathbb {R} $: Für $ a \ in \ mathbb {R} \ subset \ mathcal {P} $ wird der Logarithmus wie gewohnt definiert. Für $ a \ not \ in \ mathbb {R} $ definieren wir den Logarithmus axiomatisch: Zuerst benötigen wir $ \ ln \! \! \ Mathcal {P} $, um eine abelsche Gruppen-WRT-Addition zu sein, sogar einen Vektorraum über $ \ mathbb {R} $. Dann, für $ \ lambda \ in \ mathbb {R} $, $$ \ begin {align} \ ln (a ^ \ lambda) &: = \ lambda \ ln (a) \ end {align} $$ und für $ b \ in \ mathcal {P} $, $$ \ ln (ba): = \ ln (b) + \ ln (a). $$ Vorausgesetzt, dass $ a $ und $ b $ dieselbe Dimension haben und daher hinzugefügt werden können, gibt dies bereits den Logarithmus der Summe an: Wir wissen, dass dann $ \ x \ in \ mathbb {R} \ Doppelpunkt b = ax $ existiert Mit anderen Worten, wir können eine beliebige Summe physikalischer Größen als Produkt einer von ihnen mit einer reellen Zahl schreiben, sodass der Logarithmus beliebiger Länge auf den Logarithmus einer bestimmten Länge zuzüglich des Logarithmus des Verhältnisses zwischen den Längen reduziert wird

Zurück zu Ihrer Frage: Was ist der Logarithmus eines Kilometers? Die Antwort: $ \ ln (1 \: \ mathrm {km}) = \ ln (\ mathrm {km}) $. Wenn Sie Kilometer als Basislängeneinheit behandeln, ist dies alles, was Sie brauchen. Wenn Sie Meter oder Zoll oder was auch immer bevorzugen, erhalten Sie einfach $$ \ ln (1 \: \ mathrm {km}) = \ ln (1000 \: \ mathrm {m}) = \ ln (1000) + \ ln (\ mathrm {m}) $$$$ \ ln (1 \: \ mathrm {km}) = \ ln (\ tfrac {1 \: \ mathrm {km}} {1 "} \: \ mathrm {"}) = \ ln (\ tfrac {1 \: \ mathrm {km}} {1 "}) + \ ln (\ mathrm {"}) \ ca. 10,58 + \ ln (\ mathrm {"}) $$ Hier $ \ ln (\ mathrm {km}), \ ln (\ mathrm {m}), \ ln (\ mathrm {"}) $ sind nicht dimensionslose Zahlen. Stellen Sie sie sich eher als Elemente eines Vektorraums vor, der die reellen Zahlen als Unterraum hat.

Der beste Weg, darüber nachzudenken, ist, dass eine Zahl wie 1 km aus einer dimensionslosen 1 multipliziert mit einer Einheit, km, besteht. Wenn Sie das Protokoll eines Produkts erstellen, erhalten Sie die Summe der Protokolle. Protokoll (1 km) entspricht also Protokoll (1) + Protokoll (km). Dies zeigt, dass der Stamm von 1 km weder eine dimensionslose noch eine dimensionale Größe ist. Wenn es dimensionslos wäre, wäre es ohne Bezugnahme auf ein Einheitensystem ausdrückbar. Wenn es dimensioniert wäre, würde es sich durch Multiplikation ändern, wenn das Einheitensystem geändert würde. Es ist keines dieser Dinge.

"Logarithmus-Einheiten" sind Dezibel am nächsten, was dem 10-fachen des Basis-10-Logarithmus eines Verhältnisses entspricht. Um eine physikalische Größe in eine dezibelähnliche Einheit zu setzen, müssen Sie zuerst durch eine Referenzgröße dividieren. Zum Beispiel ist die "Dezibel" -Einheit für die Leistung "dBm", was das Verhältnis der fraglichen Leistung über 1 mW ist, ausgedrückt in dB:

$ $ P _ {\ rm dBm} = 10 \ {\ rm log_ {10}} \ left (\ frac {P _ {\ rm mW}} {1 \ \ rm mW} \ right) $$ span>

Die logarithmische Funktion kann leicht zur Transformation von einer Skala in eine andere verwendet werden. Tatsächlich ist eine Skala / Einheit ein Maß und daher nicht abschätzbar. Um sie jedoch physikalisch auszulegen, verwenden wir eine Einheit in Bezug auf einen absoluten Standard, damit der Wert sinnvoll und reproduzierbar ist. Beantworten Sie daher Ihre Frage. Log (x) ist ohne Einheit, da alle durchgeführten mathematischen Operationen an sich ohne Einheit sind. Zum besseren Verständnis möchte ich ein imaginäres Beispiel geben: "Wenn ich mit meinem Freund laufen gehe, ist der Abstand zwischen uns proportional zur Geschwindigkeit, mit der mein Freund läuft at "In diesem Beispiel sind die Einheiten auf beiden Seiten der Gleichheit völlig willkürlich, abhängig von der Formulierung der Situation. Es könnte durchaus dimensionslos sein - m / s oder sagen wir Wetter dann celsius - m / s!

Hoffe das hilft.

Für eine alternative Sicht auf die mögliche "Dimensionslosigkeit" der Logarithmusfunktion in Bezug auf ihre Beziehung zu Integralen und Ableitungen von Potenzfunktionen und ihre Nähe zur $ 0 $ -ten Potenzfunktion. Wenn man ein Primitiv berechnet von $ t ^ p $: $$ \ int t ^ p dt \ ,, $$ mit $ p \ neq -1 $ erhält man in gut festgelegten Intervallen:
$$ \ frac {1} {p +1} \ times t ^ {p + 1} \ ,. $$

Jedes Mal erhält man eine andere Dimension (oder eine Potenz für die jeweilige Einheit). Wenn Sie differenzieren, verlieren Sie Dimensionen bis zu Grad $ 0 $ für positive Kräfte. Für negative Potenzen geht dies auf $ - \ infty $ zurück: für $ p \ neq 0 $

$$ \ frac {d (t ^ p)} {dt} = pt ^ {p- 1} $$

Um die nullte Potenz herum ist definitiv etwas los.

Es ist üblich, die nullte Potenz eines Nicht-Null-Skalars $ \ alpha $ auf $ 1 $ zu setzen ($ \ alpha ^ 0 = 1 $). Wenn Sie jetzt ein Nicht-Null-$ t $ festlegen, lautet der Variationskoeffizient für eine echte $ p $ -Leistung nahe $ 0 $ wie folgt: $$ \ frac {e ^ {p \ log t} - t ^ 0} {p -0} \ approx \ frac {1 + p \ log t - 1} {p} $$, da $ p $ zu $ ​​0 $ tendiert. Daher das Verhalten von $ \ log t $ .

In gewisser Weise ist eine Konstante ein Grenzverhalten des Logarithmus oder umgekehrt. Daher sollte der Logarithmus irgendwie einheitlos sein.

Es gibt ähnliche Konzepte bei der statistischen experimentellen Datenanalyse. Wenn Sie versuchen, eine Beziehung zwischen den Variablen $ y $ und $ t $ zu finden, und keine lineare finden können, versuchen einige, mindestens eine Variable mit einer Potenzfunktion zu ändern. J. Tukey ("Erfinder" des Box-Plots und der FFT) schlug die Transformationsleiter oder Leiter der Kräfte vor, indem er $ y = a + bt ^ {p} $ betrachtete. Eine zufriedenstellendere Lösung liegt in der Box-Cox-Transformation: Wenn $ \ hat {t} $ das geometrische Mittel von $ t $ und $ \ alpha $ eine Verschiebung bezeichnet, dann gilt: $$ t_ \ alpha ^ {(p)} = \ frac {(t- \ alpha) ^ p - 1} {p \ hat {t} ^ {p-1}} $$, wobei Sie sehen, dass sorgfältig darauf geachtet wird, die gleiche "Einheit" zwischen $ t_ zu halten. \ alpha ^ {(p)} $ und $ t $. Erraten Sie, was? Für $ p = 0 $ setzen sie $ t_ \ alpha ^ {(0)} = \ hat {t} \ log (t + \ alpha) $.

Mit einem Wort, die $ 0 $ -te Potenz einer Konstanten ist $ 1 $, die $ 0 $ -te Potenz einer Variablen ist ihr $ \ log $. Irgendwie.

Referenzen:

• J. W. Tukey, Explorative Datenanalyse. Addison-Wesley, 1977.
• G. E. P. Box und D. R. Cox, Eine Analyse der Transformationen, Journal der Royal Statistical Society. Serie B, 1964.
• Verwandt mit Stackexchange: Moderner Nachfolger der exploratorischen Datenanalyse von Tukey?

Erstens ist die Frage etwas schlecht gestellt. In einem Protokolldiagramm sind die Mengen beispielsweise (log X) km und nicht log (X km) . Wir müssen die Frage weiter definieren: Was bedeutet es, "einen Logarithmus zu nehmen"? Der Logarithmus oder eine solche Funktion ist so definiert, dass er eine reelle oder komplexe Zahl nimmt und basierend auf einer bestimmten Regel eine neue Zahl angibt. Wenn Sie ihm etwas anderes als eine Zahl geben, fragen Sie ein wenig: "Wie viel wiegt die Zahl drei?". Dies ist nicht sinnvoll, da die Funktion, die das Gewicht eines Objekts angibt, keine Zahlen akzeptiert.

(Betrachten Sie physikalische Gleichungen, die physikalische Größen beinhalten, als Argumente für Logarithmen, trigonometrische Funktionen oder als Exponenten dass in Gleichungen, die sich aus der Natur ergeben, die Mengeneinheiten innerhalb von Exponenten und Funktionen immer zusammen eine dimensionslose Zahl ergeben. Jeder aussagekräftige Ausdruck muss aus dem physikalischen Denken stammen, daher müssten Sie diese Frage auch aus dem physikalischen Denken beantworten.)

Wie Ben Cromwell in seinem Kommentar feststellte, gibt es sicher Möglichkeiten, Einheiten in der Mathematik darzustellen.

Meine zwei Cent sind, dass dies eine klassische Mischung von Metaebenen ist.

Ein Kilometer ist ein Maß auf dem Boden der Erde. Wenn wir eine Karte erstellen, eine Metaebene zum tatsächlichen Maß, beträgt die Länge auf der Karte vielleicht 1 cm pro zehn Kilometer, und wir nehmen das in Kauf, ohne uns zu fragen, wie es möglich ist. Es ist möglich, weil wir sehr klar das Konzept haben, dass die Karte eine Metaebene ist.

Angenommen, wir erstellen die Karte im logarithmischen Maßstab (je nach Funktion existieren lustige Karten des Globus). Dies würde bedeuten, dass das, was auf dieser Karte als Kilometer markiert ist, logarithmisch größer wird, wenn die realen (Nicht-Meta-) Daten in Kilometern zunehmen. Der Grund, warum man Meta-Ebenen für Mengen mit Einheiten verwendet, ist der Einfachheit halber. Die Projektion des Globus auf eine Ebene ist praktisch für das, was wir tun möchten, obwohl dies die relative Größe des Kilometers auf der Karte verzerrt, die unsere "Intuition" konstant haben möchte .

Wenn wir uns mit Exponenten und Logarithmen in physikalischen Gleichungen befassen, achten wir sehr darauf, dort dimensionslose Zahlen zu haben. Es ist tatsächlich eines der Werkzeuge, Ausgleichseinheiten. Studieren Sie die Boltzmann-Verteilung als Beispiel.

Irgendwie verwirren Einheiten in der Physik die Menschen. Ein einfacher Weg, um aus dieser Verwirrung herauszukommen, besteht darin, zu erkennen, dass für die Übersetzung von Physik in Mathematik das Problem in ein Problem umgewandelt werden muss, das sich nur mit reinen (sogenannten dimensionslosen) Zahlen befasst.

Dies kann unkompliziert sein. Betrachten Sie ein einfaches Pendel. Um den Zeitraum für das Schwingen des Bob $ t_ {Swing} $ abzuleiten, müssen wir das Problem in mathematischer Form umwandeln. Dies zwingt uns, nicht mit dem Zeitraum selbst zu arbeiten, sondern mit einer dimensionslosen Größe wie dem Verhältnis zwischen $ t_ {Swing} $ und einem anderen Zeitpunkt $ t_0 $. Als Ergebnis können wir Gleichungen wie $$ \ frac {t_ {Swing}} {t_0} \ = \ f (..) $$ ableiten. Bei einem Pendel enthält das Problem einen Zeitparameter in Form der Quadratwurzel seiner Länge geteilt durch die lokale Gravitationsbeschleunigung: $ t_0 = \ sqrt {l / g} $. Man versucht also, einen Ausdruck der Form

$$ \ frac {t_ {Swing}} {\ sqrt {l / g}} \ = \ f (..) $$

Bei der Analyse für kleine Schwenkwinkel folgt $ f (..) = 2 \ pi $.

In einigen anderen Fällen reicht die Anzahl der im Problem verfügbaren Parameter nicht aus, um Machen Sie die Gleichung dimensionslos. In solchen Fällen greifen Physiker auf allgemeine physikalische Parameter zurück, die als Einheiten bezeichnet werden. Ihr einziger Zweck ist es, alle Parameter in den mathematischen Gleichungen dimensionslos zu machen (reine Zahlen).

Physiker verstoßen häufig gegen die Regel, die dimensionslose Mathematik vorschreibt. Sie werden also Gleichungen wie

$$x^2+y^2=r^2$$

sehen. Genau genommen ist dies falsch. Menschen neigen jedoch dazu, dies als Abkürzung für $$ (x / 1m) ^ 2 + (y / 1m) ^ 2 = (r / 1m) ^ 2 $$

(oder mit einer anderen Länge) zu interpretieren Einheit der Wahl im Nenner). Dies macht die Gleichung wieder dimensionslos. Ich würde argumentieren, dass das, was wirklich gemeint ist, jedoch $$ (x / r) ^ 2 + (y / r) ^ 2 = 1 $$

ist. Auch Gleichungen wie

$$ \ ln x - \ ln r = 2 \ pi $$

macht streng genommen wenig Sinn. Wieder könnten Leute diesen Unsinn in etwas Sinnvolles verwandeln, indem sie ihn als Abkürzung für

$$ \ ln (x / 1m) - \ ln (r / 1m) = 2 \ pi $$

Was jedoch wirklich gemeint ist, ist

$$ \ ln (x / r) = 2 \ pi $$

Unter dem Strich macht es keinen Sinn, eine bloße Länge $ x $ oder eine bloße Länge $ r $ in den Gleichungen zu haben. Es macht auch keinen Sinn, nur 1 Million Dollar drin zu haben. Es ist jedoch sinnvoll, einen Parameter $ \ frac {r} {1 m} $ oder $ \ frac {x} {r} $ zu haben. Dies ist immer der Fall, wird jedoch deutlicher, wenn die betreffende Funktion beispielsweise die Form eines Logarithmus annimmt.