Hier ist meine Lieblingsableitung, die ziemlich stark basiert, aber meiner Meinung nach eher einfacher ist als die in den obigen Links angegebenen. Es ist nur eine elementare Integration erforderlich!
Das Setup
Arbeiten Sie der Allgemeinheit halber an einem $ N $ -dimensionalen Raster und beschriften Sie die Rasterpunkte mit $ \ vec {n} $, einem ganzzahligen Vektor.
Angenommen, die Spannung an jedem Punkt ist $ V_ \ vec {n} $. Dann ist der Strom, der von seinen $ 2N $ -Nachbarn in $ \ vec {n} $ fließt,
$$ \ sum_ {i, \ pm} (V _ {\ vec {n} \ pm \ vec {e} _i} - V_ \ vec {n}) $$
($ \ vec {e} _i $ ist der Einheitsvektor entlang der $ i $ -Richtung.)
Bestehen Sie darauf, dass eine externe Quelle einen Ampere in $ \ vec {0} $ und aus $ \ vec {a} $ pumpt. Aktuelle Erhaltung gibt
$$ \ sum_ {i, \ pm} (V _ {\ vec {n} \ pm \ vec {e} _i} - V_ \ vec {n}) = - \ delta_ \ vec {n} + \ delta_ {\ vec {n} - \ vec {a}} $$
($ \ delta_ \ vec {n} $ entspricht $ 1 $, wenn $ \ vec {n} = \ vec {0} $ und andernfalls $ 0 $.)
Dies ist die Gleichung, die wir lösen wollen. Bei $ V_ \ vec {n} $ ist der effektive Widerstand zwischen $ \ vec {0} $ und $ \ vec {a} $ einfach
$$ R_ \ vec {a} = V_ \ vec {0} - V_ \ vec {a} $$
Leider gibt es unendlich viele Lösungen für $ V_ \ vec {n} $, und ihre Ergebnisse für $ R_ \ vec {a} $ stimmen nicht überein! Dies liegt daran, dass die Frage keine Randbedingungen im Unendlichen spezifiziert. Je nachdem, wie wir sie auswählen, können wir einen beliebigen Wert von $ R_ \ vec {a} $ erhalten, den wir mögen! Es wird sich herausstellen, dass es eine einzigartige vernünftige Auswahl gibt, aber lassen Sie uns dieses Problem zunächst vollständig vergessen und jede Lösung finden.
Lösung durch Fourier-Transformation
Die Strategie besteht darin, eine grüne Funktion $ G_ \ vec {n} $ zu finden, die
erfüllt
$$ \ sum_ {i, \ pm} (G _ {\ vec {n} \ pm \ vec {e} _i} - G_ \ vec {n}) = \ delta_ \ vec {n} $$
Eine Lösung für die ursprüngliche Gleichung wäre dann
$$ V_n = -G_ \ vec {n} + G _ {\ vec {n} - \ vec {a}} $$
Um $ G_ \ vec {n} $ zu finden, nehmen Sie an, dass es als
dargestellt werden kann
$$ G_ \ vec {n} = \ int_0 ^ {2 \ pi} \ frac {d ^ N \ vec {k}} {(2 \ pi) ^ N} (e ^ {i \ vec {k } \ cdot \ vec {n}} - 1) g (\ vec {k}) $$
Dann notiere das
\ begin {align}
\ sum_ {i, \ pm} (G _ {\ vec {n} \ pm \ vec {e} _i} - G_ \ vec {n})
& =
\ int_0 ^ {2 \ pi} \ frac {d ^ N \ vec {k}} {(2 \ pi) ^ N} e ^ {i \ vec {k} \ cdot \ vec {n}} \ left (\ sum_ {i, \ pm} e ^ {\ pm i k_i} - 2N \ right) g (\ vec {k})
\\
\ delta_ \ vec {n}
& =
\ int_0 ^ {2 \ pi} \ frac {d ^ N \ vec {k}} {(2 \ pi) ^ N} e ^ {i \ vec {k} \ cdot \ vec {n}}
\ end {align}
Wir sehen, dass die Gleichung für $ G_ \ vec {n} $ durch Auswahl von
gelöst werden kann
$$ g (\ vec {k}) = \ frac {1} {\ sum_ {i, \ pm} e ^ {\ pm k_i} - 2N} $$
was zu
führt
$$ G_ \ vec {n} = \ frac {1} {2} \ int_0 ^ {2 \ pi} \ frac {d ^ N \ vec {k}} {(2 \ pi) ^ N} \ frac {\ cos (\ vec {k} \ cdot \ vec {n}) - 1} {\ sum \ cos (k_i) - N} $$
Übrigens scheint das lustige $ -1 $ im Zähler nicht viel anderes zu tun, als $ G_ \ vec {n} $ um eine $ \ vec {n} $ - unabhängige Konstante zu verschieben, also Sie könnte sich fragen, was es dort tut. Aber ohne es wäre das Integral unendlich, zumindest für $ N \ leq 2 $.
Die endgültige Antwort lautet also
$$ R_ \ vec {a} = V_ \ vec {0} - V_ \ vec {a} = 2 (G_ \ vec {a} - G_ \ vec {0}) = \ int_0 ^ {2 \ pi } \ frac {d ^ N \ vec {k}} {(2 \ pi) ^ N} \ frac {1 - \ cos (\ vec {k} \ cdot \ vec {a})} {N - \ sum \ cos (k_i)} $$
Warum ist das die richtige Antwort?
(Ab diesem Zeitpunkt ist $ N = 2 $)
Ich habe vorhin gesagt, dass es unendlich viele Lösungen für $ V_ \ vec {n} $ gibt. Das obige ist jedoch etwas Besonderes, da sich die Spannungen und Ströme in großen Entfernungen $ r $ vom Ursprung wie
verhalten
$$ V = \ mathcal {O} (1 / r) \ qquad I = \ mathcal {O} (1 / r ^ 2) $$
Ein Standardsatz (Eindeutigkeit von Lösungen zur Laplace-Gleichung) besagt, dass es nur eine Lösung geben kann, die diese Bedingung erfüllt. Unsere Lösung ist also die einzigartige mit dem geringstmöglichen Stromfluss im Unendlichen und mit $ V_ \ infty = 0 $ . Und selbst wenn die Frage nicht danach gefragt hat, ist es offensichtlich die einzig vernünftige Sache, die gestellt werden muss.
Oder doch? Vielleicht möchten Sie das Problem lieber definieren, indem Sie an einem endlichen Raster arbeiten, dort die eindeutige Lösung für $ V_ \ vec {n} $ finden und dann versuchen, eine Grenze zu setzen, wenn die Rastergröße unendlich wird. Man kann jedoch argumentieren, dass das aus einem Raster der Größe $ L $ erhaltene $ V_ \ vec {n} $ mit einem Fehler in der Reihenfolge $ 1 / L $ zu unserem $ V_ \ vec {n} $ konvergieren sollte. Das Endergebnis ist also dasselbe.
Integrale ausführen
Betrachten Sie zuerst den diagonalen Fall
\ begin {align}
R_ {n, n}
& = \ frac {1} {(2 \ pi) ^ 2} \ int_A dx \, dy \, \ frac {1 - \ cos (n (x + y))} {2 - \ cos (x) - \ cos (y)} \\
& = \ frac {1} {2 (2 \ pi) ^ 2} \ int_A dx \, dy \, \ frac {1 - \ cos (n (x + y))} {1 - \ cos (\ frac { x + y} {2}) \ cos (\ frac {xy} {2})}
\ end {align}
wobei $ A $ das Quadrat $ 0 \ leq x, y \ leq 2 \ pi $ ist.
Da der Integrand periodisch ist, kann die Domäne wie folgt von $ A $ in $ A '$ geändert werden:
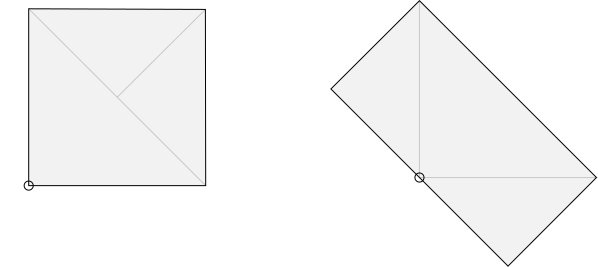
Ändern Sie dann die Variablen in
$$ a = \ frac {x + y} {2} \ qquad b = \ frac {x-y} {2} \ qquad dx \, dy = 2 \, da \, db $$
das Integral wird
$$ R_ {n, n} = \ frac {1} {(2 \ pi) ^ 2} \ int_0 ^ \ pi da \ int _ {- \ pi} ^ \ pi db \, \ frac {1 - \ cos (2na)} {1 - \ cos (a) \ cos (b)} $$
Das $ b $ -Integral kann mit der Halbbräunungssubstitution
durchgeführt werden
$$ t = \ tan (b / 2) \ qquad \ cos (b) = \ frac {1-t ^ 2} {1 + t ^ 2} \ qquad db = \ frac {2} {1+ t ^ 2} dt $$
geben
$$ R_ {n, n} = \ frac {1} {2 \ pi} \ int_0 ^ \ pi da \, \ frac {1 - \ cos (2na)} {\ sin (a)} $$
Die Triggeridentität
$$ 1 - \ cos (2na) = 2 \ sin (a) \ big (\ sin (a) + \ sin (3a) + \ dots + \ sin ((2n-1) a) \ big) $$
reduziert das verbleibende $ a $ -Integral auf
\ begin {align}
R_ {n, n}
& =
\ frac {2} {\ pi} \ left (1 + \ frac {1} {3} + \ dots + \ frac {1} {2n-1} \ right)
\ end {align}
Induktion
Während eine Integration erforderlich war, um die Diagonalwerte von $ R_ {m, n} $ zu erhalten, kann der Rest ohne diese ermittelt werden. Der Trick besteht darin, Rotations- / Reflexionssymmetrie zu verwenden,
$$ R_ {n, m} = R _ {\ pm n, \ pm m} = R _ {\ pm m, \ pm n} $$
zusammen mit der folgenden Wiederholungsrelation
$$ R_ {n + 1, m} + R_ {n-1, m} + R_ {n, m + 1} + R_ {n, m-1} - 4 R_ {n, m} = 2 \ delta _ {(n, m)} $$
, das mit $ R_ \ vec {n} = 2 G_ \ vec {n} $ und der Definitionsgleichung für $ G_ \ vec {n} $ abgeleitet werden kann.
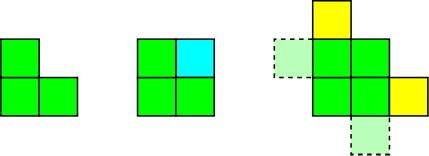
Beginnen Sie mit der trivialen Aussage, dass
$$ R_ {0,0} = 0 $$
Das Anwenden der Wiederholungsrelation bei $ (0,0) $ und das Verwenden der Symmetrie ergibt
$$ R_ {1,0} = R_ {0,1} = 1/2 $$
Die nächste Zeile wird wie folgt ausgeführt
Und der danach ...
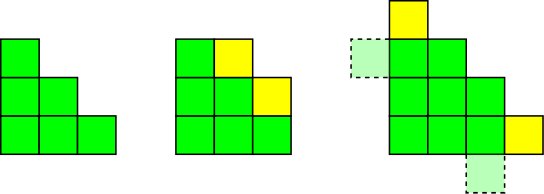
Das wiederholte Abwechseln der beiden obigen Schritte ergibt einen Algorithmus zum Bestimmen jedes $ R_ {m, n} $. Es ist klar, dass alle die Form
haben
$$ a + b / \ pi $$
wobei $ a $ und $ b $ rationale Zahlen sind. Jetzt kann dieser Algorithmus leicht von Hand ausgeführt werden, aber man kann ihn auch in Python codieren:
importiere numpy als np
Bruchteile importieren als fr
N = 4
arr = np.empty ((N * 2 + 1, N * 2 + 1, 2), dtype = 'Objekt')
def plus (i, j):
arr [i + 1, j] = 4 * arr [i, j] - arr [i - 1, j] - arr [i, j + 1] - arr [i, abs (j - 1)]
def sogar (i):
arr [i, i] = arr [i - 1, i - 1] + [0, fr.Fraction (2, 2 * i - 1)]
für k im Bereich (1, i + 1): plus (i + k - 1, i - k)
def ungerade (i):
arr [i + 1, i] = 2 * arr [i, i] - arr [i, i - 1]
für k im Bereich (1, i + 1): plus (i + k, i - k)
arr [0, 0] = 0
arr [1, 0] = [fr.Fraction (1, 2), 0]
für i im Bereich (1, N):
selbst ich)
ungerade (i)
gerade (N)
für i im Bereich (0, N + 1):
für j im Bereich (0, N + 1):
a, b = arr [max (i, j), min (i, j)]
print ('(', a, ') + (', b, ') / π', sep = '', end = '\ t')
drucken()
Dies erzeugt die Ausgabe
$$
\ Groß
\ begin {array} {| c: c: c: c: c}
40 - \ frac {368} {3 \ pi} & \ frac {80} {\ pi} - \ frac {49} {2} & 6 - \ frac {236} {15 \ pi} & \ frac {24} {5 \ pi} - \ frac {1} {2} & \ frac {352} {105 \ pi} \\
\ hdashline
\ frac {17} {2} - \ frac {24} {\ pi} & \ frac {46} {3 \ pi} - 4 & \ frac {1} {2} + \ frac {4} {3 \ pi } & \ frac {46} {15 \ pi} & \ frac {24} {5 \ pi} - \ frac {1} {2} \\
\ hdashline
2 - \ frac {4} {\ pi} & \ frac {4} {\ pi} - \ frac {1} {2} & \ frac {8} {3 \ pi} & \ frac {1} {2}+ \ frac {4} {3 \ pi} & 6 - \ frac {236} {15 \ pi} \\
\ hdashline
\ frac {1} {2} & \ frac {2} {\ pi} & \ frac {4} {\ pi} - \ frac {1} {2} & \ frac {46} {3 \ pi} - 4& \ frac {80} {\ pi} - \ frac {49} {2} \\
\ hdashline
0 & \ frac {1} {2} & 2 - \ frac {4} {\ pi} & \ frac {17} {2} - \ frac {24} {\ pi} & 40 - \ frac {368} {3 \ pi} \\
\ hline
\ end {array}
$$
von dem wir die endgültige Antwort ablesen können,
$$ R_ {2,1} = \ frac {4} {\ pi} - \ frac {1} {2} $$